Bond Markets, Analysis and Strategies, 8/E Frank J. Fabozzi solutions manual
CHAPTER 2
PRICING OF BONDS
CHAPTER SUMMARY
This chapter will focus on the time value of money and how to calculate the price of a bond. When pricing a bond it is necessary to estimate the expected cash flows and determine the appropriate yield at which to discount the expected cash flows. Among other aspects of a bond, we will look at the reasons why the price of a bond changes
REVIEW OF TIME VALUE OF MONEY
Money has time value because of the opportunity to invest it at some interest rate.
Future Value
The future value of any sum of money invested today is:
Pn = P0(1 + r)n
where n = number of periods, Pn = future value n periods from now (in dollars), P0 = original principal (in dollars), r = interest rate per period (in decimal form), and the expression (1 + r)n represents the future value of $1 invested today for n periods at a compounding rate of r.
When interest is paid more than one time per year, both the interest rate and the number of periods used to compute the future value must be adjusted as follows:
r = annual interest rate / number of times interest paid per year, and
n = number of times interest paid per year times number of years.
The higher future value when interest is paid semiannually, as opposed to annually, reflects the greater opportunity for reinvesting the interest paid.
Future Value of an Ordinary Annuity
When the same amount of money is invested periodically, it is referred to as an annuity. When the first investment occurs one period from now, it is referred to as an ordinary annuity.
The equation for the future value of an ordinary annuity is:
where A is the amount of the annuity (in dollars).
Example of Future Value of an Ordinary Annuity Using Annual Interest:
If A = $2,000,000, r = 0.08, and n = 15, then Pn = è P15 =
= $2,000,000[27.152125] = $54,304.250.
Because 15($2,000,000) = $30,000,000 of this future value represents the total dollar amount of annual interest payments made by the issuer and invested by the portfolio manager, the balance of $54,304,250 – $30,000,000 = $24,304,250 is the interest earned by reinvesting these annual interest payments.
Example of Future Value of an Ordinary Annuity Using Semiannual Interest:
Consider the same example, but now we assume semiannual interest payments.
If A = $2,000,000 / 2 = $1,000,000, r = 0.08 / 2 = 0.04, n = 2(15) = 30, then
= $1,000,000[56.085] = $56,085,000.
The opportunity for more frequent reinvestment of interest payments received makes the interest earned of $26,085,000 from reinvesting the interest payments greater than the $24,304,250 interest earned when interest is paid only one time per year.
Present Value
The present value is the future value process in reverse. We have:
For a given future value at a specified time in the future, the higher the interest rate (or discount rate), the lower the present value. For a given interest rate (discount rate), the further into the future that the future value will be received, then the lower its present value.
Present Value of a Series of Future Values
To determine the present value of a series of future values, the present value of each future value must first be computed. Then these present values are added together to obtain the present value of the entire series of future values.
Present Value of an Ordinary Annuity
When the same dollar amount of money is received each period or paid each year, the series is referred to as an annuity. When the first payment is received one period from now, the annuity is called an ordinary annuity. When the first payment is immediate, the annuity is called an annuity due.
The present value of an ordinary annuity is:
where A is the amount of the annuity (in dollars).
The term in brackets is the present value of an ordinary annuity of $1 for n periods.
Example of Present Value of an Ordinary Annuity Using Annual Interest:
If A = $100, r = 0.09, and n = 8, then: 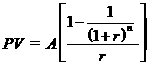

Present Value When Payments Occur More Than Once Per Year
If the future value to be received occurs more than once per year, then the present value formula is modified so that (i) the annual interest rate is divided by the frequency per year, and (ii) the number of periods when the future value will be received is adjusted by multiplying the number of years by the frequency per year.
PRICING A BOND
Determining the price of any financial instrument requires an estimate of (i) the expected cash flows, and (ii) the appropriate required yield. The required yield reflects the yield for financial instruments with comparable risk, or alternative investments.
The cash flows for a bond that the issuer cannot retire prior to its stated maturity date consist of periodic coupon interest payments to the maturity date, and the par (or maturity) value at maturity.
In general, the price of a bond can be computed using the following formula:
where P = price (in dollars), n = number of periods (number of years times 2), C = semiannual coupon payment (in dollars), r = periodic interest rate (required annual yield divided by 2),
M = maturity value, and t = time period when the payment is to be received.
Computing the Value of a Bond: An Example:
Consider a 20-year 10% coupon bond with a par value of $1,000 and a required yield of 11%. Given C = 0.1($1,000) / 2 = $50, n = 2(20) = 40 and r = 0.11 / 2 = 0.055, the present value of the coupon payments is:
The present value of the par or maturity value of $1,000 is: =
=
= $117.46.
The price of the bond (P) = present value coupon payments + present value maturity value
= $802.31 + $117.46 = $919.77.
Pricing Zero-Coupon Bonds
For zero-coupon bonds, the investor realizes interest as the difference between the maturity value and the purchase price. The equation is:
where M is the maturity value. Thus, the price of a zero-coupon bond is simply the present value of the maturity value.
Zero-Coupon Bond Example
Consider the price of a zero-coupon bond that matures 15 years from now, if the maturity value is $1,000 and the required yield is 9.4%. Given M = $1,000, r = 0.094 / 2 = 0.047,
and n = 2(15) = 30, we have: =
=
= $252.12.
Price-Yield Relationship
A fundamental property of a bond is that its price changes in the opposite direction from the change in the required yield. The reason is that the price of the bond is the present value of the cash flows.
Relationship Between Coupon Rate, Required Yield, and Price
When yields in the marketplace rise above the coupon rate at a given point in time, the price of the bond falls so that an investor buying the bond can realizes capital appreciation. The appreciation represents a form of interest to a new investor to compensate for a coupon rate that is lower than the required yield. When a bond sells below its par value, it is said to be selling at a discount. A bond whose price is above its par value is said to be selling at a premium.
Relationship Between Bond Price and Time if Interest Rates Are Unchanged
For a bond selling at par value, the coupon rate is equal to the required yield. As the bond moves closer to maturity, the bond will continue to sell at par value. Its price will remain constant as the bond moves toward the maturity date.
The price of a bond will not remain constant for a bond selling at a premium or a discount. The discount bond increases in price as it approaches maturity, assuming that the required yield does not change. For a premium bond, the opposite occurs. For both bonds, the price will equal par value at the maturity date.
Reasons for the Change in the Price of a Bond
The price of a bond can change for three reasons: (i) there is a change in the required yield owing to changes in the credit quality of the issuer; (ii) there is a change in the price of the bond selling at a premium or a discount, without any change in the required yield, simply because the bond is moving toward maturity; or, (iii) there is a change in the required yield owing to a change in the yield on comparable bonds (i.e., a change in the yield required by the market).
COMPLICATIONS
The framework for pricing a bond assumes the following: (i) the next coupon payment is exactly six months away; (ii) the cash flows are known; (iii) the appropriate required yield can be determined; and, (iv) one rate is used to discount all cash flows.
Next Coupon Payment Due in Less than Six Months
When an investor purchases a bond whose next coupon payment is due in less than six months, the accepted method for computing the price of the bond is as follows:
where v = (days between settlement and next coupon) / (days in six-month period).
Cash Flows May Not Be Known
For most bonds, the cash flows are not known with certainty. This is because an issuer may call a bond before the stated maturity date.
Determining the Appropriate Required Yield
All required yields are benchmarked off yields offered by Treasury securities. From there, we must still decompose the required yield for a bond into its component parts.
One Discount Rate Applicable to All Cash Flows
A bond can be viewed as a package of zero-coupon bonds, in which case a unique discount rate should be used to determine the present value of each cash flow.
PRICING FLOATING-RATE AND INVERSE-FLOATING-RATE SECURITIES
The cash flow is not known for either a floating-rate or an inverse-floating-rate security; it will depend on the reference rate in the future.
Price of a Floater
The coupon rate of a floating-rate security (or floater) is equal to a reference rate plus some spread or margin. The price of a floater depends on (i) the spread over the reference rate and
(ii) any restrictions that may be imposed on the resetting of the coupon rate.
Price of an Inverse Floater
In general, an inverse floater is created from a fixed-rate security. The security from which the inverse floater is created is called the collateral. From the collateral two bonds are created: a floater and an inverse floater.
The price of a floater depends on (i) the spread over the reference rate and (ii) any restrictions that may be imposed on the resetting of the coupon rate. For example, a floater may have a maximum coupon rate called a cap or a minimum coupon rate called a floor. The price of a floater will trade close to its par value as long as the spread above the reference rate that the market requires is unchanged, and neither the cap nor the floor is reached.
The price of an inverse floater equals the collateral’s price minus the floater’s price.
PRICE QUOTES AND ACCRUED INTEREST
Price Quotes
A bond selling at par is quoted as 100, meaning 100% of its par value. A bond selling at a discount will be selling for less than 100; a bond selling at a premium will be selling for more than 100.
Accrued Interest
When an investor purchases a bond between coupon payments, the investor must compensate the seller of the bond for the coupon interest earned from the time of the last coupon payment to the settlement date of the bond. This amount is called accrued interest. For corporate and municipal bonds, accrued interest is based on a 360-day year, with each month having 30 days.
The amount that the buyer pays the seller is the agreed-upon price plus accrued interest. This is often referred to as the full price or dirty price. The price of a bond without accrued interest is called the clean price. The exceptions are bonds that are in default. Such bonds are said to be quoted flat, that is, without accrued interest.
KEY POINTS
· The price of a bond is the present value of the bond’s expected cash flows, the discount rate being equal to the yield offered on comparable bonds. For an option-free bond, the cash flows are the coupon payments and the par value or maturity value. The higher (lower) the required yield, the lower (higher) the price of a bond.
· For a zero-coupon bond, there are no coupon payments. The price of a zero-coupon bond is equal to the present value of the maturity value, where the number of periods used to compute the present value is double the number of years and the discount rate is a semiannual yield.
· A bond’s price changes in the opposite direction from the change in the required yield. The reason is that as the required yield increases (decreases), the present value of the cash flow decreases (increases).
· A bond will be priced below, at par, or above par depending the bond’s coupon rate and the required yield required by investors. When the coupon rate is equal to the required yield, the bond will sell at its par value. When the coupon rate is less (greater) than the required yield, the bond will sell for less (more) than its par value.
· Over time, the price of a premium or discount bond will change even if the required yield does not change. Assuming that the credit quality of the issuer is unchanged, the price change on any bond can be decomposed into a portion attributable to a change in the required yield and a portion attributable to the time path of the bond.
· The price of a floating-rate bond will trade close to par value if the spread required by the market does not change and there are no restrictions on the coupon rate.
· The price of an inverse floater depends on the price of the collateral from which it is created and the price of the floater.
· Accrued interest is the amount that a bond buyer who purchases a bond between coupon payments must pay the bond seller. The amount represents the coupon interest earned from the time of the last coupon payment to the settlement date of the bond.
ANSWERS TO QUESTIONS FOR CHAPTER 2
(Questions are in bold print followed by answers.)
1. A pension fund manager invests $10 million in a debt obligation that promises to pay 7.3% per year for four years. What is the future value of the $10 million?
To determine the future value of any sum of money invested today, we can use the future value equation, which is: Pn = P0 (1 + r)n where n = number of periods, Pn = future value n periods from now (in dollars), P0 = original principal (in dollars) and r = interest rate per period (in decimal form). Inserting in our values, we have: P4 = $10,000,000(1.073)4 = $10,000,000(1.325558466)
= $13,255,584.66.
2. Suppose that a life insurance company has guaranteed a payment of $14 million to a pension fund 4.5 years from now. If the life insurance company receives a premium of $10.4 million from the pension fund and can invest the entire premium for 4.5 years at an annual interest rate of 6.25%, will it have sufficient funds from this investment to meet the $14 million obligation?
To determine the future value of any sum of money invested today, we can use the future value equation, which is: Pn = P0 (1 + r)n where n = number of periods, Pn = future value n periods from now (in dollars), P0 = original principal (in dollars) and r = interest rate per period (in decimal form). Inserting in our values, we have: P4.5 = $10,400,000(1.0625)4.5 = $10,400,000(1.313651676)
= $13,661,977.43. Thus, it will be short by: $13,661,977.43 – $14,000,000 = -$338,022.57.
3. Answer the below questions.
(a) The portfolio manager of a tax-exempt fund is considering investing $500,000 in a debt instrument that pays an annual interest rate of 5.7% for four years. At the end of four years, the portfolio manager plans to reinvest the proceeds for three more years and expects that for the three-year period, an annual interest rate of 7.2% can be earned. What is the future value of this investment?
At the end of year four, the portfolio manager’s amount is given by: Pn = P0 (1 + r)n. Inserting in our values, we have P4 = $500,000(1.057)4 = $500,000(1.248245382) = $624,122.66. In three more years at the end of year seven, the manager amount is given by: P7 = P4(1 + r)3. Inserting in our values, we have: P7 = $624,122.66(1.072)3 = $624,122.66(1.231925248) = $768,872.47.
(b) Suppose that the portfolio manager in Question 3, part a, has the opportunity to invest the $500,000 for seven years in a debt obligation that promises to pay an annual interest rate of 6.1% compounded semiannually. Is this investment alternative more attractive than the one in Question 3, part a?
At the end of year seven, the portfolio manager’s amount is given by the following equation, which adjusts for semiannual compounding. We have: Pn = P0(1 + r/2)2(n). Inserting in our values, we have P7 = $500,000(1 + 0.061/2)2(7) = $500,000(1.0305)14 = $500,000(1.522901960) = $761,450.98. Thus, this investment alternative is not more attractive. It is less by the amount of $761,450.98 – $768,872.47 = -$7,421.49.
4. Suppose that a portfolio manager purchases $10 million of par value of an eight-year bond that has a coupon rate of 7% and pays interest once per year. The first annual coupon payment will be made one year from now. How much will the portfolio manager have if she (1) holds the bond until it matures eight years from now, and (2) can reinvest all the annual interest payments at an annual interest rate of 6.2%?
At the end of year eight, the portfolio manager’s amount is given by the following equation, which adjusts for annual compounding. We have:
where A = coupon rate times par value. Inserting in our values, we have:
+ $10,000,000 = $700,000[9.9688005] + $10,000,000
= $6,978,160.38 + $10,000,000 = $16,978,160.38.
5. Answer the below questions.
(a) If the discount rate that is used to calculate the present value of a debt obligation’s cash flow is increased, what happens to the price of that debt obligation?
The price will fall. A fundamental property of a bond is that its price changes in the opposite direction from the change in the required yield. The reason is that the price of the bond is the present value of the cash flows. As the required yield increases, the present value of the cash flow decreases; thus the price decreases. The opposite is true when the required yield decreases: The present value of the cash flows increases, and therefore the price of the bond increases.
(b) Suppose that the discount rate used to calculate the present value of a debt obligation’s cash flow is x%. Suppose also that the only cash flows for this debt obligation are $200,000 four years from now and $200,000 five years from now. For which of these cash flows will the present value be greater?
Cash flows that come earlier will have a greater value. As long as x% is positive and the amount is the same, the present value will be greater for the $200,000 four years from now compared to five years from now. This can also be seen by noting that if x > 0 then 

6. The pension fund obligation of a corporation is calculated as the present value of the actuarially projected benefits that will have to be paid to beneficiaries. Why is the interest rate used to discount the projected benefits important?
It is important because the present value increases as the discount rate (or interest rate) decreases and it decreases as the discount rate increases. Thus, in order to project the benefits accurately, we need an accurate estimate of the discount rate. If we underestimate the discount rate then we will be projecting more available pension funds than we will actually have.
7. A pension fund manager knows that the following liabilities must be satisfied:
| Years from Now | Liability (in millions) |
| 1 | $2.0 |
| 2 | $3.0 |
| 3 | $5.4 |
| 4 | $5.8 |
Suppose that the pension fund manager wants to invest a sum of money that will satisfy this liability stream. Assuming that any amount that can be invested today can earn an annual interest rate of 7.6%, how much must be invested today to satisfy this liability stream?
To satisfy year one’s liability (n = 1), the pension fund manager must invest an amount today that is equal to the future value of $2.0 million at 7.6%. We have:
To satisfy year two’s liability (n = 2), the pension fund manager must invest an amount today that is equal to the future value of $3.0 million at 7.6%. We have:
To satisfy year three’s liability (n = 3), the pension fund manager must invest an amount today that is equal to the future value of $5.4 million at 7.6%. We have:
To satisfy year four’s liability (n = 4), the pension fund manager must invest an amount today that is equal to the future value of $5.8 million at 7.6%. We have:
If we add the four present values, we get $1,858,736.06 + $2,591,174.80 + $4,334,679.04 + $4,326,920.42 = $13,111,510.32, which is the amount the pension fund manager needs to invest today to cover the liability stream for the next four years.
8. Calculate for each of the following bonds the price per $1,000 of par value assuming semiannual coupon payments.
| Bond | Coupon Rate (%) | Years to Maturity | Required Yield (%) |
| A | 8 | 9 | 7 |
| B | 9 | 20 | 9 |
| C | 6 | 15 | 10 |
| D | 0 | 14 | 8 |
Consider a 9-year 8% coupon bond with a par value of $1,000 and a required yield of 7%. Given C = 0.08($1,000) / 2 = $40, n = 2(9) = 18 and r = 0.07 / 2 = 0.035, the present value of the coupon payments is:
The present value of the par or maturity value of $1,000 is: =
=
=
$538.361. Thus, the price of the bond (P) = present value of coupon payments + present value of par value = $527.587 + $538.361 = $1,065.95.
Consider a 20-year 9% coupon bond with a par value of $1,000 and a required yield of 9%. Given C = 0.09($1,000) / 2 = $45, n = 2(20) = 40 and r = 0.09 / 2 = 0.045, the present value of the coupon payments is:
= $45[18.401584] = $828.071.
The present value of the par or maturity value of $1,000 is: =
=
=
$171.929. Thus, the price of the bond (P) = $828.071 + $171.929 = $1,000.00. [NOTE. We already knew the answer would be $1,000 because the coupon rate equals the yield to maturity.]
Consider a 15-year 6% coupon bond with a par value of $1,000 and a required yield of 10%. Given C = 0.06($1,000) / 2 = $30, n = 2(15) = 30 and r = 0.10 / 2 = 0.05, the present value of the coupon payments is:
= $30[15.372451] = $461.174.
The present value of the par or maturity value of $1,000 is: =
=
=
$231.377. Thus, the price of the bond (P) = $461.174 + $231.377 = $692.55.
Consider a 14-year 0% coupon bond with a par value of $1,000 and a required yield of 8%. Given C = 0($1,000) / 2 = $0, n = 2(14) = 28 and r = 0.08 / 2 = 0.04, the present value of the coupon payments is:
= $0[16.66306322] = $0. [NOTE. We already knew the answer because the coupon rate is zero.]
The present value of the par or maturity value of $1,000 is: =
=
= $333.48. Thus, the price of the bond (P) = $0 + $333.48 = $333.48.
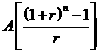


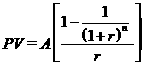



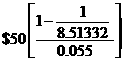


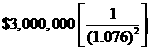
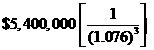

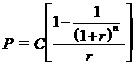

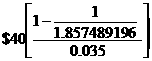
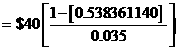


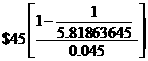
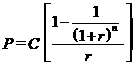





No comments:
Post a Comment