Business Statistics: A First Course 6th edition solutions manual and test bank by David M. Levine
CHAPTER 2
2.1 The answer depends on the chosen data set.
2.2 The answer depends on the specific story.
2.3 The supermarket chain should use primary data collected through an observation study of the shopping behavior of their customers.
2.4 The information presented there is based on surveys.
2.5 (a) Category Frequency Percentage
A 13 26%
B 28 56
C 9 18
(b) Category “B” is the majority.
2.6 (a) Table frequencies for all student responses
Student Major Categories
Gender A C M Totals
Male 14 9 2 25
Female 6 6 3 15
Totals 20 15 5 40
(b) Table percentages based on overall student responses
Student Major Categories
Gender A C M Totals
Male 35.0% 22.5% 5.0% 62.5%
Female 15.0% 15.0% 7.5% 37.5%
Totals 50.0% 37.5% 12.5% 100.0%
Table based on row percentages
Student Major Categories
Gender A C M Totals
Male 56.0% 36.0% 8.0% 100.0%
Female 40.0% 40.0% 20.0% 100.0%
Totals 50.0% 37.5% 12.5% 100.0%
Table based on column percentages
Student Major Categories
Gender A C M Totals
Male 70.0% 60.0% 40.0% 62.5%
Female 30.0% 40.0% 60.0% 37.5%
Totals 100.0% 100.0% 100.0% 100.0%
2.7 (a)
| Category | Frequency | Percentage |
| Flammables/Irritants | 8,350 | 59.26% |
| Knives and blades | 4,134 | 29.34% |
| Prohibited tools | 753 | 5.34% |
| Sharp objects | 497 | 3.53% |
| Other | 357 | 2.53% |
| Total | 14,091 | 100.00% |
(b) Flammables, irritants, knives and blades made up almost 90% of the banned items.
2.8 (a)
| Region | Oil Consumption | Percentage |
| (millions of barrels a day) | ||
| Developed Europe | 14.5 | 17.18% |
| Japan | 4.4 | 5.21% |
| United States | 18.8 | 22.27% |
| Rest of the world | 46.7 | 55.33% |
| Total | 84.4 | 100.00% |
(b) More than half the oil consumed is from countries other than the U.S., Japan, and developed Europe. More than 20% is consumed by the U.S. and slightly less than 20% is consumed by developed Europe.
2.9 (a)
| Category | Cost per Household | Percentage |
| Civil servant retirement | 15,851 | 2.90% |
| Federal debt | 54,537 | 9.97% |
| Medicare | 284,288 | 52.00% |
| Military retirement | 29,694 | 5.43% |
| Social Security | 160,216 | 29.30% |
| Other | 2,172 | 0.40% |
| Total | 546,758 | 100.00% |
(b) Medicare at 52% and Social Security at 29.3% together made up more than 80% of the debt.
Teaching Tips for
Business Statistics: A First Course, Sixth Edition
Educational Philosophy
In our many years of teaching business statistics, we have continually searched for ways to improve the teaching of business statistics courses. We actively participate in Decision Sciences Institute (DSI), American Statistical Association (ASA), and Making Statistics More Effective in Schools and Business (MSMESB) conferences. We use the Guidelines for Assessment and Learning (GAISE) reports as well as our reflections on teaching busines statistics to a diverse group of students at several large universities. These experiences have shaped our vision that has come to include these key principles:
1. Students need to be shown the relevance of statistics.
• Students need a frame of reference when learning statistics, especially when statistics is not their major. That frame of reference for business students should be the functional areas of business—accounting, finance, information systems, management, and marketing. Each statistical topic needs to be presented in an applied context related to at least one of these functional areas.
• The focus in teaching each topic should be on its application in business, the interpretation of results, the presentation of assumptions, the evaluation of the assumptions, and the discussion of what should be done if the assumptions are violated.
2. Students need to be familiar with the software used in the business world.
• Integrating spreadsheet and/or statistical software into all aspects of an introductory statistics course allows the course to focus on interpretation of results instead of computations.
• Introductory business statistics courses should recognize that in business, spreadsheet software is typically available on a decision-maker’s desktop and statistical software is often also available.
3. Students need to be given sufficient guidance on using software.
• Textbooks should provide enough instructions so that students can effectively use the software integrated with the study of statistics, without having the software instruction dominate the course.
4. Students need ample practice in order to understand how statistics is used in business.
• Both classroom examples and homework exercises should involve actual or realistic data as much as possible.
• Students should work with data sets, both small and large, and be encouraged to look beyond the statistical analysis of data to the interpretation of results in a managerial context.
Chapter 1
One way to begin the course is by discussing why a businessperson needs to know about statistics. This will provide a reason for why the student has been required to take this course. The first day is extremely important to driving out preexisting fear that some students have concerning the course. You should talk about the fact that this course is different from a mathematics course in that you will not be deriving any proofs, but instead will be focusing on how statistics can be used in the different functional areas of business. You can talk a little about the DCOVA problem solving approach that will be used starting in Chapter 2 as a way of solving problems that will occur on the job when students graduate.
This can be followed by a brief explanation of the basic vocabulary of statistics including the distinction between descriptive and inferential statistics. Then you need to discuss the types of variables. Be sure to discuss the different types carefully since the ability to distinguish between categorical and numerical data will be crucial later in the course. Go over examples of each type of variable and have students provide examples of each type.
At this time, if you are going to use Microsoft® Excel, ask the class whether they are familiar with Microsoft® Excel. Depending on the degree to which the instructor wishes to integrate Excel into the course, point out that, since most managers will have integrated products such as Microsoft® Office on their desktops, it would be useful to understand how Excel can be used to analyze data. If you are going to use Minitab, you can talk about statistical packages and the advantages of using them instead of or in addition to using Excel in certain circumstances.
The chapter also introduces a continuing case related to the Managing Ashland MultiComm Services that appears at the end of many chapters. The Digital cases are introduced in this chapter also. In these cases, students visit Web sites related to companies and issues raised in the Using Statistics scenarios that start each chapter. The goal of the Digital cases is for students to develop skills needed to identify misuses of statistical information. As would be the situation with many real world cases, in Digital cases students often need to sift through claims and assorted information in order to discover the data most relevant to a case task. They will then have to examine whether the conclusions and claims are supported by the data. (Instructional tips for using the Managing Ashland MultiComm Services and Digital cases and solutions to the Managing Ashland MultiComm Services and Digital cases are included in this Instructor’s Solutions Manual.).
If you are using Excel, make sure that students read the Excel Guide at the end of the chapter. The first section explains the different types of Excel instructions. The In-Depth Excel instructions provide step-by-step instructions and live worksheets that automatically update when data changes. These instructions can also be used with Mac Excel and OpenOffice.org Calc 3. The PHStat2 add-in instructions provide instructions for using the PHStat2 add-in. Analysis ToolPak instructions provide instructions for using the Analysis ToolPak, the Excel add-in packages with many versions of Excel.
The reminder of the Excel Guide in this chapter goes over Excel basics including entering data, opening and saving workbooks, creating, printing, and copying worksheets, cell references, and entering formulas. Those students with limited knowledge of Excel should read Appendix B and F and all students should read Appendices C, D, and G.
If you are using Minitab, make sure that students read the Minitab Guide at the end of the chapter. Topics covered include entering data, opening, creating, and saving worksheets and projects, and printing projects and/or worksheets. Those students with limited knowledge of computers should read Appendix B.
Chapter 2
This book uses a systematic approach for meeting a business objective or solving a business problem. This approach goes across all the topics in the book and most importantly can be used as a framework in real world situations when students graduate. The approach has the acronym DCOVA, which stands for Define, Collect, Organize, Visualize, and Analyze.
- Define the business objective or problem to be solved and then define the variables to be studied.
- Collect the data from appropriate sources
- Organize the data
- Visualize the data by developing charts
- Analyze the data by using statistical methods to reach conclusions.
You can begin by emphasizing the importance of defining your objective or problem. Go back to the importance of operational definitions of variables discussed in Chapter 1 and the importance of knowing the type for each variable.
Continue by discussing the need for collecting data and then introduce sources of data including the World Wide Web. Next, if you are going to collect sample data to use in Chapters 2 and 3, you can illustrate the need for sampling by conducting a survey of students in your class (otherwise leave the discussion of sampling until chapter 7). Ask each student to collect his or her own personal data concerning the time it takes to get ready to go to class in the morning or the time it takes to get to school or home from school. First, ask the students to write down a definition of how they plan to measure this time. Then, collect the various answers and read them to the class. Then, a single definition could be provided (such as the time to get ready is the time measured from when you get out of bed to when you leave your dorm or home, recorded to the nearest minute). In the next class, select a random sample of students and use the data collected (depending on the sample size) in class when Chapters 2 and 3 are discussed.
Then, move on to the Organize step that involves setting up your data in an Excel (or Minitab) worksheet and developing tables to help you prepare charts and analyze your data. Begin your discussion for categorical data with the example on p. 28 on how people pay their bills. Show the summary table and then if you wish, explain that you can sometimes organize the data into a two-way table that has one variable in the row and another in the column.
Continue with organizing data (but now for numerical data) by referring to the cost of a restaurant meal on p. 32. Show the simple ordered array and how a frequency distribution, percentage distribution, or cumulative distribution can summarize the raw data in a way that is more useful.
Now you are ready to tackle the Visualize step. A good way of starting this part of the chapter is to display the following quote.
"A picture is worth a thousand words."
Students will almost certainly be familiar with Microsoft® Word and may have already used Excel to construct charts that they have pasted into Word documents. Now you will be using either Excel or Minitab to construct many different types of charts. Return to the bill payment data previously discussed and illustrate how a bar chart and pie chart can be constructed. Mention their advantages and disadvantages. A good example is to show the data on incomplete ATM transactions on p. 43 and how the Pareto chart enables you to focus on the vital few categories. If time permits, you can discuss the side-by-side bar chart for a contingency table.
To examine charts for numerical variables you can either use the restaurant data previously mentioned or data that you have collected from your class. You may want to begin with a simple stem-and-leaf display that both organizes the data and shows a bar type chart. Then move on to the histogram and the various polygons, pointing out the advantages and disadvantages of each.
If time permits, you can discuss the scatter plot and the time-series plot for two numerical variables. Otherwise, you can wait until you get to regression analysis later in the semester. Also, if time permits, you can discuss how multidimensional tables allow you to drill down to individual cells of the table.
If the opportunity is available, we believe that it is worth the time to cover Section 2.8 on Misuses and Common Errors in Visualizing Data. This is a topic that students very much enjoy since it allows for a great deal of classroom interaction. After discussing the fundamental principles of good graphs, try to illustrate some of the improper displays shown in Figures 2.23 – 2.25. Ask students what is “bad” about these figures. Follow up with a homework assignment involving Problems 2.60 – 2.65 (USA Today is a great source).
You will find that the chapter review problems provide large data sets with numerous variables. Report writing exercises, the team project, and the student survey database provide the opportunity for students to integrate written and or oral presentation with the statistics they have learned.
The Managing Ashland MultiComm Services case enables students to examine the use of statistics in an actual business environment. The Digital case refers to the EndRun Financial Services and claims that have been made.
The Excel and Minitab Guides for this and the remaining chapters are organized according to the sections of the chapter. These guides are quite extensive since they cover both organizing and visualizing many different graphs. The Excel Guide includes instructions for In-Depth Excel, PHStat2, and the Analysis ToolPak. Pick and choose the approaches that you prefer.
Chapter 3
This chapter on descriptive numerical statistical measures represents the initial presentation of statistical symbols in the text. Students who need to review arithmetic and algebraic concepts may wish to refer to Appendix A for a quick review or to appropriate texts (see www.pearson.com) or videos (www.videoaidedinstruction.com). Once again, as with the tables and charts constructed for numerical data, it is useful to provide an interesting set of data for classroom discussion. If a sample of students was selected earlier in the semester and data concerning student time to get ready or commuting time was collected (see Chapters 1 and 2), use these data in developing the numerous descriptive summary measures in this chapter. (If they have not been developed, obtain other data for classroom illustration.)
Discussion of the chapter begins with the property of central tendency. We have found that almost all students are familiar with the arithmetic mean (which they know as the average) and most students are familiar with the median. A good way to begin is to compute the mean for your classroom example. Emphasize the effect of extreme values on the arithmetic mean and point out that the mean is like the center of a seesaw -- a balance point. Note that you will return to this concept later when you discuss the variance and the standard deviation. You might want to introduce summation notation at this point and express the arithmetic mean in formula notation as in Equation (3.1). (Alternatively, you could wait until you cover the variance and standard deviation.) A classroom example in which summation notation is reviewed is usually worthwhile. Remind the students again that Appendix A includes a review of arithmetic and algebra and summation notation [or refer them to other text sources such as those found at www.pearson.com or videos (see www. videoaidedinstruction.com)].
The next statistic to compute is the median. Be sure to remind the students that the median as a measure of position must have all the values ranked in order from lowest to highest. Be sure to have the students compare the arithmetic mean to the median and explain that this tells us something about another property of data (skewness). Following the median, the mode can be briefly discussed. Once again, have the students compare this result to those of the arithmetic mean and median for your data set.
The completion of the discussion of central tendency leads to the second characteristic of data, variability. Mention that all measures of variation have several things in common: (1) they can never be negative, (2) they will be equal to 0 when all items are the same, (3) they will be small when there isn't much variation, and (4) they will be large when there is a great deal of variation.
The first measure of variability to consider is the simplest one, the range. Be sure to point out that the range only provides information about the extremes, not about the distribution between the extremes. Point out that the range lacks one important ingredient, the ability to take into account each data value. Bring up the idea of computing the differences around the mean, but then return to the fact that as the balance point of the seesaw, these differences add up to zero. At that point, ask the students what they can do mathematically to remove the negative sign for some of the values. Most likely, they will answer by telling you to square them (although someone may realize that the absolute value could be taken). Next, you may want to define the squared differences as a sum of squares. Now you need to have the students realize that the number of values being considered affects the magnitude of the sum of squared differences. Therefore, it makes sense to divide by the number of values and compute a measure called the variance. If a population is involved, you divide by N, the population size, but if you are using a sample, you divide by n - 1, to make the sample result a better estimate of the population variance. You can finish the development of variation by noting that since the variance is in squared units, you need to take the square root to compute the standard deviation.
Another measure of variation that can be discussed is the coefficient of variation. Be sure to illustrate the usefulness of this as a measure of relative variation by using an example in which two data sets have vastly different standard deviations, but also vastly different means. A good example is one that involves the volatility of stock prices. Point out that the variation of the price should be considered in the context of the magnitude of the arithmetic mean. At this point you may want to have the students use the Visual Explorations in Exploring Descriptive Statistics procedure (see p. 107). By changing values in the data provided, students can observe how the mean, median, and standard deviation are affected.
The final measure of variation is the Z score. Point out that this provides a measure of variation in standard deviation units. You can also say that you will return to Z scores in Chapter 6 when the normal distribution will be discussed.
You are now ready to move on to the third characteristic of data, shape. Be sure to clearly define and illustrate both symmetric and skewed distributions by comparing the mean and median.
Once these three characteristics have been discussed, you are ready to show how they can be computed using Excel or Minitab.
Now that these measures of central tendency and variation are understood, you can further explore data by computing the quartiles, the interquartile range, the five-number summary, and constructing a boxplot. You begin by determining the quartiles. Reference here can be made to the standardized exams that most students have taken, and the quantile scores that they have received (97th percentile, 48th percentile, and 12th percentile). Explain that the 1st and 3rd quartiles are merely two special quantiles -- the 25th and 75th, that unlike the median (the 2nd quartile), are not at the center of the distribution. Once the quartiles have been computed, the interquartile range can be determined. It is useful to note that the interquartile range computes the variation in the center of the distribution as compared to the difference in the extremes computed by the range.
You can then mention the five-number summary of minimum value, first quartile, median, third quartile, and maximum value. Then, you construct the boxplot. Present this plot from the perspective of serving as a tool for determining the location, variability, and symmetry of a distribution by visual inspection, and as a graphical tool for comparing the distribution of several groups. It is useful to display Figure 3.6 on page 114 that indicates the shape of the boxplot for four different distributions. Then, use PHStat2 or Minitab to construct a boxplot. Note that you can construct the boxplot for a single group or for multiple groups.
If you desire, you can discuss descriptive measures for a population and introduce the empirical rule and the Chebyshev rule.
If time permits, and you have covered scatter plots in Chapter 2, you can briefly discuss the covariance and the coefficient of correlation as a measure of the strength of the association between two numerical variables. Point out that the coefficient of correlation has the advantage as compared to the covariance of being on a scale that goes from -1 to +1. Figure 3.9 on p. 124 is useful in depicting scatter plots for different coefficients of correlation.
Once again, you will find that the chapter review problems provide large data sets with numerous variables. Report writing exercises, the team project, and the survey database provide the opportunity for students to integrate written and or oral presentation with the statistics they have learned.
The Managing Ashland MultiComm Services case enables students to examine the use of descriptive statistics in an actual business environment. The Digital case continues the evaluation of the EndRun Financial Services discussed in the Digital case in Chapter 2.
The Excel Guide for the chapter includes instructions on using different Excel functions to compute various statistics. Alternatively, you can use the Analysis ToolPak to compute a list of many statistics. PHStat2 can be used to construct a boxplot. The Minitab Guide includes instructions for various descriptive statistics and boxplots.
Chapter 4
The chapter on probability represents a bridge between the descriptive statistics already covered and the topics of statistical inference, regression, and quality improvement to be covered in subsequent chapters. In many traditional statistics courses, often a great deal of time is spent on probability topics that are of little direct applicability in basic statistics. The approach in this text is to cover only those topics that are of direct applicability in the remainder of the text.
You need to begin with a relatively concise discussion of some probability rules. Essentially, students really just need to know that (1) no probability can be negative, (2) no probability can be more than 1, and (3) the sum of the probabilities of a set of mutually exclusive events adds to 1.0. Students often understand the subject best if it is taught intuitively with a minimum of formulas, with an example that relates to a business application shown as a two-way contingency table (see the Using Statistics example). If desired, you can use In-Depth Excel or PHStat2 to compute probabilities from the contingency table.
Once these basic elements of probability have been discussed, if there is time and you desire, conditional probability and Bayes’ theorem can be covered. The Think About This concerning email SPAM is a wonderful way of helping student realize the application of probability to everyday life. Be aware that in a one-semester course where time is particularly limited, these topics may be of marginal importance. In addition, you may wish to spend a bit of time going over counting rules, especially if the binomial distribution will be covered in Chapter 5.
The Digital case in this chapter extends the evaluation of the EndRun Financial Services to consider claims made about various probabilities.
Chapter 5
Now that the basic principles of probability have been discussed, the probability distribution is developed and the expected value and variance (and standard deviation) are computed and interpreted. Given that a probability distribution has been defined, you can now discuss some specific distributions. Although every introductory course undoubtedly covers the normal distribution to be discussed in Chapter 6, the decision about whether to cover the binomial or Poisson distributions is matter of personal choice and depends on whether the course is part of a two-course sequence.
If the binomial distribution is covered, an interesting way of developing the binomial formula is to follow the Using Statistics example that involves an accounting information system. Note, in this example, the value for p is 0.10. (It is best not to use an example with p = 0.50 since this represents a special case). The discussion proceeds by asking how you could get three tagged order forms in a sample of 4. Usually a response will be elicited that provides three items of interest out of four selections in a particular order such as Tagged Tagged Not Tagged Tagged. Ask the class, what would be the probability of getting Tagged on the first selection? When someone responds 0.1, ask them how they found that answer and what would be the probability of getting Tagged on the second selection. When they answer 0.1 again, you will be able to make the point that in saying 0.1 again, they are assuming that the probability of Tagged stays constant from trial to trial. When you get to the third selection and the students respond 0.9, point out that this is a second assumption of the binomial distribution -- that only two outcomes are possible -- in this case Tagged and Not Tagged, and the sum of the probabilities of Tagged and Not Tagged must add to 1.0. Now you can compute the probability of three out of four in this order by multiplying (0.1)(0.1)(0.9)(0.1) to get 0.0036. Ask the class if this is the answer to the original question. Point out that this is just one way of getting three Tagged out of four selections in a specific order, and, that there are four ways to get three Tagged out of four selections This leads to the development of the binomial formula Equation (5.5). You might want to do another example at this point that calls for adding several probabilities such as three or more Tagged, less than three Tagged, etc. Complete the discussion of the binomial distribution with the computation of the mean and standard deviation of the distribution. Be sure to point out that for samples greater than five, computations can become unwieldy and the student should use PHStat2, the BINOMDIST function in Excel, Minitab, or the binomial tables (See the Online Binomial.pdf tables).
Once the binomial distribution has been covered, if time permits, you can cover the Poisson distribution. Point out the distinction between the binomial and Poisson distributions. Note that the Poisson is based on an area of opportunity in which you are counting occurrences within an area such as time or space. Contrast this with the binomial distribution in which each value is classified as of interest or not of interest. Point out the equations for the mean and standard deviation of the Poisson distribution and indicate that the mean is equal to the variance. Since the computation of probabilities from these discrete probability distributions can become tedious for other than small sample sizes, it is important to discuss PHStat2, the POISSON Excel function, or Minitab.
The Managing Ashland MultiComm Services case for this chapter relates to the binomial distribution.
Chapter 6
Now that probability and probability distributions have been discussed in Chapters 4 and 5, you are ready to introduce the normal distribution. We recommend that you begin by mentioning some reasons that the normal distribution is so important and discuss several of its properties. We would also recommend that you do not show Equation (6.1) in class as it will just intimidate some students. You might begin by focusing on the fact that any normal distribution is defined by its mean and standard deviation and display Figure 6.3 on p. 204. Then, an example can be introduced and you can explain that if you subtracted the mean from a particular value, and divided by the standard deviation, the difference between the value and the mean would be expressed as a standardized normal or Z score that was discussed in Chapter 3. Next, use Table E.2, the cumulative normal distribution, to find probabilities under the normal curve. In the text, the cumulative normal distribution is used since this table is consistent with results provided by Excel and Minitab. (The standardized normal distribution is shown in Table E.9) Make sure that all the students can find the appropriate area under the normal curve in their cumulative normal distribution tables. If anyone cannot, show them how to find the correct value. Be sure to remind the class that since the total area under the curve adds to 1.0, the word area is synonymous with the word probability. Once this has been accomplished, a good approach is to work through a series of examples with the class, having a different student explain how to find each answer. The example that will undoubtedly cause the most problems will be finding the values corresponding to known probabilities. Slowly go over the fact that in this type of example, the probability is known and the Z value needs to be determined, which is the opposite of what the student has done in previous examples. Also point out that in cases in which the unknown X value is below the mean, the negative sign must be assigned to the Z value. Once the normal distribution has been covered, you can use PHStat2, various Excel functions, or Minitab to compute normal probabilities. It is also useful to use the Visual Explorations Exploring the Normal Distribution procedure on p. 213. This will be useful if you intend to use examples that explore the effect on the probabilities obtained by changing the X value, the population mean, m, or the standard deviation,s. The Think About This essay provides a historical perspective of the application of the normal distribution.
If you have sufficient time in the course, the normal probability plot can be discussed. Be sure to note that all the data values need to be ranked in order from lowest to highest and that each value needs to be converted to a normal score. Again, you can either use PHStat2 to generate a normal probability plot or use Excel functions and the Chart Wizard or use Minitab.
The Managing Ashland MultiComm Services case for this chapter relates to the normal distribution. The Digital case involves the normal distribution and the normal probability plot.
Chapter 7
You should spend some time discussing sampling, even if it is just using the table of random numbers to select a random sample. You may want to take a bit more time and discuss the types of survey sampling methods and issues involved with survey sampling results. The Think About This essay discusses the important issue of the use of Web-based surveys.
The coverage of the normal distribution in Chapter 6 flows into a discussion of sampling distributions. Point out the fact that the concept of the sampling distribution of a statistic is important for statistical inference. Make sure that students realize that problems in this section will find probabilities concerning the mean, not concerning individual values. It is helpful to display Figure 7.5 on p. 242 to show how the Central Limit Theorem applies to differently shaped populations. A useful classroom or homework exercise involves using PHStat2 or Excel to form sampling distributions. This reinforces the concept of the Central Limit Theorem.
The Managing Ashland MultiComm Services case for this chapter relates to the sampling distribution of the mean. The Digital case involves the sampling distribution of the mean.
Chapter 8
You should begin this chapter by reviewing the concept of the sampling distribution covered in Chapter 7. It is important that the students realize that (1) an interval estimate provides a range of values for the estimate of the population parameter, (2) you can never be sure that the interval developed does include the population parameter, and (3) the proportion of intervals that include the population parameter within the interval is equal to the confidence level.
Note that the Using Statistics example for this chapter, which refers to the Saxon Home Improvement Company is actually a case study that relates to every part of the chapter. This scenario is a good candidate for use as the classroom example demonstrating an application of statistics in accounting. It also enables you to use the DCOVA approach of Define, Collect, Organize, Visualize, and Analyze in the context of statistical inference.
When introducing the t distribution for the confidence interval estimate of the population mean, be sure to point out the differences between the t and normal distributions, the assumption of normality, and the robustness of the procedure. It is useful to display Table E.3 in class to illustrate how to find the critical t value. When developing the confidence interval for the proportion, remind the students that the normal distribution may be used here as an approximation to the binomial distribution as long as the assumption of normality is valid [when np and n(1 - p) are at least 5].
Having covered confidence intervals, you can move on to sample size determination by turning the initial question of estimation around, and focusing on the sample size needed for a desired confidence level and width of the interval. In discussing sample size determination for the mean, be sure to focus on the need for an estimate of the standard deviation. When discussing sample size determination for the proportion, be sure to focus on the need for an estimate of the population proportion and the fact that a value of p = 0.5 can be used in the absence of any other estimate. Since the formulas for the confidence interval estimates and sample sizes discussed in this chapter are straightforward, using PHStat2 or In-Depth Excel can remove much of the tedious nature of these computations.
The Managing Ashland MultiComm Services case for this chapter involves developing various confidence intervals and interpreting the results in a marketing context. The Digital case also relates to confidence interval estimation.
Chapter 9
A good way to begin the chapter is to focus on the reasons that hypothesis testing is used. We believe that it is important for students to understand the logic of hypothesis testing before they delve into the details of computing test statistics and making decisions. If you begin with the Using Statistics example concerning the filling of cereal boxes, slowly develop the rationale for the null and alternative hypotheses. Ask the students what conclusion they would reach if a sample revealed a mean of 200 grams (They will all say that something is the matter) and if a sample revealed a mean of 367.99 grams (Almost all will say that the difference between the sample result and what the mean is supposed to be is so small that it must be due to chance). Be sure to make the point that hypothesis testing allows you to take away the decision from a person's subjective judgment, and enables you to make a decision while at the same time quantifying the risks of different types of incorrect decisions. Be sure to go over the meaning of the Type I and Type II errors, and their associated probabilities a and b along with the concept of statistical power.
Set up an example of a sampling distribution such as Figure 9.1 on p. 298, and show the regions of rejection and nonrejection. Explain that the sampling distribution and the test statistic involved will change depending on the characteristic being tested. Focus on the situation where s is unknown if you have numerical data. Emphasize that s is virtually never known. It is also useful at this point to introduce the concept of the p-value approach as an alternative to the classical hypothesis testing approach. Define the p-value and use the phrase given in the text “If the p-value is low, Ho must go.” and the rules for rejecting the null hypothesis and indicate that the p-value approach is a natural approach when using Excel or Minitab, since the p-value can be determined by using PHStat, Excel functions, the Data Analysis tool or Minitab.
Once the initial example of hypothesis testing has been developed, you need to focus on the differences between the tests used in various situations. The Chapter 9 summary table is useful for this since it presents a road map for determining which test is used in which circumstance. Be sure to point out that one-tail tests are used when the alternative hypothesis involved is directional (e.g., m > 368, p < 0.20). Examine the effect on the results of changing the hypothesized mean or proportion.
Both the Managing Ashland MultiComm Services case and the Digital case involve the use of the one-sample test of hypothesis for the mean.
Chapter 10
This chapter discusses tests of hypothesis for the differences between two or more means and between two proportions. The chapter begins with t tests for the difference between the means, then covers the Z test for the difference between two proportions, the F test for the ratio of two variances, and concludes with the one way Analysis of Variance to test the difference among more than two means.
The first test of hypothesis covered is usually the test for the difference between the means of two groups for independent samples. Point out that the test statistic involves pooling of the sample variances from the two groups and assumes that the population variances are the same for the two groups. Students should be familiar with the t distribution, assuming that the confidence interval estimate for the mean has been previously covered. Point out that a stem-and-leaf display, a boxplot, or a normal probability plot can be used to evaluate the validity of the assumptions of the t test for a given set of data. This allows you to once again use the DCOVA approach of Define, Collect, Organize, Visualize, and Analyze to meet a business objective.
Once the t test has been discussed, you can use the Excel worksheets provided with the In-Depth Excel approach, PHStat2, the Data Analysis tool or Minitab to determine the test statistic and p-value. Mention that if the variances are not equal, a separate variance t test can be conducted. The Think About This essay is a wonderful example of how the two-sample t test was used to solve a business problem that a student had after she graduated and had taken the introductory statistics course.
At this point, having covered the test for the difference between the means of two independent groups, you can discuss a test that examines differences in the means of two paired or matched groups. The key difference is that the focus in this test is on differences between the paired values in the two groups since the data have been collected from matched pairs or repeated measurements on the same individuals or items. Once the paired t test has been discussed, the In-Depth Excel approach, PHStat2, the Data Analysis tool, or Minitab can be used to determine the test statistic and p-value.
You can continue the coverage of differences between two groups by testing for the difference between two proportions. Be sure to review the difference between numerical and categorical data emphasizing the categorical variable used here classifies each observation as of interest or not of interest. Make sure that the students realize that the test for the difference between two proportions follows the normal distribution. A good classroom example involves asking the students if they enjoy shopping for clothing and then classifying the yes and no responses by gender. Since there often will be a difference between males and females, you can then ask the class how we might go about determining whether the results are statistically significant.
The F-test for the variances can be covered next. Be sure to carefully explain that this distribution, unlike the normal and t distributions, is not symmetric and cannot have a negative value since the statistic is the ratio of two variances. Remind the students that the larger variance is in the numerator. Be sure to mention that a boxplot of the two groups and normal probability plots can be used to determine the validity of the assumptions of the F test. This is particularly important here since this test is sensitive to non-normality in the two populations. The In-Depth Excel approach, PHStat2, the Data Analysis tool or Minitab can be used to determine the test statistic and p-value.
If the one-way ANOVA F test for the difference between c means is to be covered in your course, a good way to start is to go back to the sum of squares concept that was originally covered when the variance and standard deviation were introduced in Section 3.2. Explain that in the one-way Analysis of Variance, the sum of squared differences around the overall mean can be divided into two other sums of squares that add up to the total sum of squares. One of these measures differences among the means of the groups and thus is called sum of squares among groups (SSA), while the other measures the differences within the groups and is called the sum of squares within the groups (SSW). Be sure to remind the students that, since the variance is a sum of squares divided by degrees of freedom, a variance among the groups and a variance within the groups can be computed by dividing each sum of squares by the corresponding degrees of freedom. Make the point that the terminology used in the Analysis of Variance for variance is Mean Square, so the variances computed are called MSA, MSW, and MST. This will lead to the development of the F statistic as the ratio of two variances. A useful approach at this point when all formulas are defined, is to set up the ANOVA summary table. Try to minimize the focus on the computations by reminding students that the Analysis of Variance computations can be done using In-Depth Excel, PHStat2, the Data Analysis tool or Minitab. It is also useful to show how to obtain the critical F value by either referring to Table E.5 or the Excel or Minitab results. Be sure to mention the assumptions of the Analysis of Variance and that the boxplot and normal probability plot can be used to evaluate the validity of these assumptions for a given set of data. Levene’s test can be used to test for the equality of variances. In-Depth Excel, PHStat2, or Minitab can be used to compute the results for this test.
Once the Analysis of Variance has been covered, if time permits (which it may not in a one-semester course), you will want to determine which means are different. Although many approaches are available, this text uses the Tukey-Kramer procedure that involves the Studentized range statistic shown in Table E.6. Be sure that students compare each paired difference between the means to the critical range. Note that you can use In-Depth Excel, PHStat2, or Minitab to compute Tukey-Kramer multiple comparisons.
Be aware that the Managing Ashland MultiComm Services case involves all the sections of the chapter except the test for the difference between two proportions since it contains both independent sample and matched sample aspects. The Digital case is based on two or more independent samples. Thus, only the sections on the t test for independent samples, the F test for the difference between two variances, and the one way ANOVA are involved.
Chapter 11
This chapter covers chi-square tests. The Using Statistics example concerning hotels relates to all three sections of the chapter.
If you covered the Z test for the difference between two proportions in Chapter 10, you can return to the example you used there and point out that the chi-square test can be used as an alternative. A good classroom example involves asking the students if they enjoy shopping for clothing (or revisiting Chapter 10’s example) and then classifying the yes and no responses by gender. Since there often will be a difference between males and females, you can then ask the class how they might go about determining whether the results are statistically significant. The expected frequencies are computed by finding the mean proportion of items of interest (enjoying shopping) and items not of interest (not enjoying shopping) and multiplying by the sample sizes of males and females respectively. This leads to the computation of the test statistic. Once again as with the case of the normal, t, and F distribution, be sure to set up a picture of the chi-square distribution with its regions of rejection and non-rejection and critical values. In addition, go over the assumptions of the chi square test including the requirement for an expected frequency of at least five in each cell of the 2 × 2 contingency table.
Now you are ready to extend the chi-square test to more than two groups. Be sure to discuss the fact that with more than two groups, the number of degrees of freedom will change and the requirements for minimum cell expected frequencies will be somewhat less restrictive.
The discussion of the chi-square test concludes with the test of independence in the r by c table. Be sure to go over the interpretation of the null and alternative hypotheses and how they differ from the situation in which there are only two rows. You can use In-Depth Excel, PHStat2, or Minitab.
The Managing Ashland MultiComm Services case extends the survey discussed in Chapter 8 to analyze data from contingency tables. The Digital case also involves analyzing various contingency tables.
Chapter 12
Regression analysis is probably the most widely used and misused statistical method in business and economics. You may want to start the chapter with the Think About This essay on p. 471 to show students the importance of this topic in business. In an era of easily available statistical and spreadsheet applications, we believe that the best approach is one that focuses on the interpretation of regression results obtained from such applications, the assumptions of regression, how those assumptions can be evaluated, and what can be done if they are violated. Although we also feel that is useful for students to work out at least one example with the aid of a hand calculator, we believe that the focus on hand calculations should be minimized.
A good way to begin the discussion of regression analysis is to focus on developing a model that can provide a better prediction of a variable of interest. The Using Statistics example, which forecasts sales for a clothing store, is useful for this purpose. You can extend the DCOVA approach discussed earlier by defining the business objective, discussing data collection, and data organization before moving on to the visualization and analysis in this chapter. Be sure to clearly define the dependent variable and the independent variable at this point.
Once the two types of variables have been defined, the example should be introduced. Explain the goal of the analysis and how regression can be useful. Follow this with a scatter plot of the two variables. Before developing the Least Squares method, review the straight-line formula and note that different notation is used in statistics for the intercept and the slope than in mathematics. At this point, you need to develop the concept of how the straight line that best fits the data can be found. One approach involves plotting several lines on a scatter plot and asking the students how they can determine which line fits the data better than any other. This usually leads to a criterion that minimizes the differences between the actual Y value and the value that would be predicted by the regression line. Remind the class that when you computed the mean in Chapter 3, you found out that the sum of the differences around the mean was equal to zero. Tell the class that the regression line in two dimensions is similar to the mean in one dimension, and that the differences between the actual Y value and the value that would be predicted by the regression line will sum to zero. Students at this point, having covered the variance, will usually tell you just to square the differences. At this juncture, you might want to substitute the regression equation for the predicted value, and tell the students that since you are minimizing a quantity, derivatives are used. We discourage you from doing the actual proof, but mentioning derivatives may help some students realize that the calculus they may have learned in mathematics courses is actually used to develop the theory behind the statistical method. The least-squares concepts discussed can be reinforced by using the Visual Explorations in Exploring Simple Linear Regression Coefficients procedure on p. 440. This procedure produces a scatter plot of the site selection data of Table 12.1 with an unfitted line of regression and a floating control panel of controls with which to adjust the line. The spinner buttons can be used to change the values of the slope and Y intercept to change the line of regression. As these values are changed, the difference from the minimum SSE changes.
The solution obtained from the Least Squares method allows you to find the slope and Y intercept. In this text, since the emphasis is on the interpretation of computer output, focus is now on finding the regression coefficients on the output shown in Figure 12.4 on p. 436. Once this has been done, carefully review the meaning of these regression coefficients in the problem involved. The coefficients can now be used to predict the Y value for a given X value. Be sure to discuss the problems that occur if you try to extrapolate beyond the range of the X variable. Now you can show how to use either the In-Depth Excel, the Analysis ToolPak, PHStat2, or Minitab to obtain the regression output.
Tell the students that now you need to determine the usefulness of the regression model by subdividing the total variation in Y into two component parts, explained variation or regression sum of squares (SSR) and unexplained variation or error sum of squares (SSE). Once the sum of squares has been determined and the coefficient of determination r2 computed, be sure to focus on the interpretation. Having computed the error sum of squares (SSE), the standard error of the estimate can be computed. Make the analogy that the standard error of the estimate has the same relationship to the regression line that the standard deviation had to the arithmetic mean.
The completion of this initial model development phase allows you to begin focusing on the validity of the model fitted. First, go over the assumptions and emphasize the fact that unless the assumptions are evaluated, a correct regression analysis has not been carried out. Reiterate the point that this is one of the things that people are most likely to do incorrectly when they carry out a regression analysis.
Once the assumptions have been discussed, you are ready to begin evaluating whether they are true for the model that has been fit. This leads into a discussion of residual analysis. Emphasize that Excel or Minitab can be used to determine the residuals and that in determining whether there is a pattern in the residuals, you look for gross patterns that are obvious on the plot, not minor patterns that are not obvious. Be sure to note that the residual plot can also be used to evaluate the assumption of equal variance along with whether there is a pattern in the residuals over time if the data have been collected in sequential order. Point out that finding no pattern (i.e., a random pattern) means that the model fit is an appropriate one. However, it does not mean that other alternative models involving additional variables should not be considered. Mention also, that a normal probability plot of the residuals can be helpful in determining the validity of the normality assumption. If time permits, the discussion of the Anscombe data in Section 12.9 serves as a strong reinforcement of the importance of residual analysis.
If time is available, you may wish to discuss the Durbin-Watson statistic for autocorrelation. Be sure to discuss how to find the critical values from the table of the D statistic and the fact that sometimes the results will be inconclusive.
Once the model fit has been found to be appropriate, inferences in regression can be made. First cover the t or F test for the slope by referring to the Excel or Minitab results. Here, the p-value approach is usually beneficial. Then, if time permits, you can discuss the confidence interval estimate for the mean and the prediction interval for the individual value.
Both the Managing Ashland MultiComm Services case and the Digital case involve a simple linear regression analysis of a set of data.
To perform simple linear regression, you can use In-Depth Excel, the Analysis ToolPak , PHStat2, or Minitab.
Chapter 13
If time is available in the course, you can now move on to multiple regression. You should point out that Microsoft Excel or Minitab needs to be used to perform the computations in multiple regression. Once you have the results, you need to focus on the interpretation of the regression coefficients and how the interpretation differs between simple linear regression and multiple regression. Mention the aspects of multiple regression that are similar in interpretation to those observed in simple regression -- prediction, residual analysis, coefficient of determination, and standard error of the estimate. If sufficient time is available, it is probably most efficiently used in covering the dummy variable model. With dummy variables, be sure to mention that the categories must be coded as 0 and 1. In addition, indicate the importance of determining whether there is an interaction between the dummy variable and the other independent variables. Further discussion can include interaction terms in regression models.
Both the Managing Ashland MultiComm Services case and the Digital case involve developing a multiple regression model that includes dummy variables.
Chapter 14 (Online)
In order to fully understand the role of statistics in quality management, the themes of quality management and Six Sigma need to be mentioned. Although students may wonder why this is either being discussed in a statistics class (or why they are reading non-statistical material), they usually enjoy learning about this subject since it provides a rationale for how the statistics course relates to management.
You may want to begin the discussion of control charts by demonstrating the Red Bead experiment. Tell the students that two broad categories of control charts will be considered, attribute charts in Sections 14.2 and variables charts in Section 14.4.
Once this introduction has been completed, an overview of the theory of control charts can be undertaken. Begin by referring to the normal distribution and mention Shewhart's concern about committing errors in determining special causes. Tell the students that setting the limits at three standard deviation units away from the mean is done to insure that there is only a small chance that a stable process will have special cause signals that appear and cannot be explained. Continue the discussion by noting that the integer value 3 made computations simpler in an era prior to the availability of calculators and computers, and that experience has shown that this serves the purpose of keeping false alarms to a minimum.
Once these topics have been discussed, you are ready to begin covering specific control charts. The choice of where to start is an individual one. The simplest approach is to begin with the p chart and refer to the Red Bead experiment and then use other examples such as those shown in Section 14.2. Be sure that students are aware that Excel, PHStat2, or Minitab can be used to construct the p chart
The discussion of variables charts should begin with a review of the distinction between attribute and variables charts. Briefly discuss the decisions that need to be made when sample sizes are to be determined and subgroups are to be formed. Be sure to emphasize the fact that variables charts are usually done in pairs, one for the variability and the other for the mean. Emphasize the notion that if the variability chart is out of control, you will be unable to meaningfully interpret the chart for the mean. Again, note that Excel, PHStat2, or Minitab can be used to construct both R and charts.
The themes of quality management and the inclusion of a discussion of the work of Deming and Shewhart allow you to distinguish between common causes of variation and special causes of variation. Perhaps the best way to reinforce this is by conducting the Red Bead experiment (see Section 14.3). This experiment allows the student to see the distinction between the two types of variation. The amount of time spent on Sections 14.5 and 14.6 is a matter of instructor discretion. Some may wish to just list the fourteen points and have students read the section, while others will want to cover the points in detail. Regardless of which approach is taken, in order to emphasize the importance of statistics, the Shewhart-Deming PDSA cycle needs to be mentioned since the study stage typically involves the use of statistical methods. In addition, points 6 (institute training on the job) and 13 (encourage education and self-improvement for everyone) underscore the importance of everyone within an organization being familiar with the basic statistical methods required to manage a process. Students find the experiment of counting Fs (see Figure 14.8) particularly intriguing since they can't believe that they have messed up such a seemingly easy set of directions.
The importance of statistics can be reinforced by briefly covering the Six Sigma®, an approach that is being used by many large corporations. Go over the DMAIC model and compare it to Deming’s 14 points.
The Harnswell Company Sewing Machine Company case contains several phases and uses R and charts. The Managing Ashland MultiComm Services case also has several phases and uses the p chart and R and
charts.
Business Statistics: A First Course, 6e (Levine)
Chapter 2 Organizing and Visualizing Data
1) Jared was working on a project to look at global warming and accessed an Internet site where he captured average global surface temperatures from 1866. Which of the four methods of data collection was he using?
A) published sources
B) experimentation
C) surveying
D) observation
Answer: A
Difficulty: Easy
Keywords: sources of data
2) The British Airways Internet site provides a questionnaire instrument that can be answered electronically. Which of the four methods of data collection is involved when people complete the questionnaire?
A) published sources
B) experimentation
C) surveying
D) observation
Answer: C
Difficulty: Easy
Keywords: sources of data
3) A marketing research firm, in conducting a comparative taste test, provided three types of peanut butter to a sample of households randomly selected within the state. Which of the four methods of data collection is involved when people are asked to compare the three types of peanut butter?
A) published sources
B) experimentation
C) surveying
D) observation
Answer: B
Difficulty: Easy
Keywords: sources of data
4) Tim was planning for a meeting with his boss to discuss a raise in his annual salary. In preparation, he wanted to use the Consumer Price Index to determine the percentage increase in his real (inflation-adjusted) salary over the last three years. Which of the four methods of data collection was involved when he used the Consumer Price Index?
A) published sources
B) experimentation
C) surveying
D) observation
Answer: A
Difficulty: Easy
Keywords: sources of data
5) Which of the four methods of data collection is involved when a person counts the number of cars passing designated locations on the Los Angeles freeway system?
A) published sources
B) experimentation
C) surveying
D) observation
Answer: D
Difficulty: Moderate
Keywords: sources of data
6) A statistics student found a reference in the campus library that contained the median family incomes for all 50 states. She would report her data collection method as
A) a designed experiment.
B) observational data.
C) a random sample.
D) a published source.
Answer: D
Difficulty: Easy
Keywords: sources of data
7) The personnel director at a large company studied the eating habits of the company's employees. The director noted whether employees brought their own lunches to work, ate at the company cafeteria, or went out to lunch. The goal of the study was to improve the food service at the company cafeteria. This type of data collection would best be considered as
A) an observational study.
B) a designed experiment.
C) a random sample.
D) a quota sample.
Answer: A
Difficulty: Easy
Keywords: sources of data
8) A study attempted to estimate the proportion of Florida residents who were willing to spend more tax dollars on protecting the beaches from environmental disasters. Twenty-five hundred Florida residents were surveyed. What type of data collection procedure was most likely used to collect the data for this study?
A) a designed experiment
B) a published source
C) a random sample
D) observational data
Answer: C
Difficulty: Easy
Keywords: sources of data
TABLE 2-1
An insurance company evaluates many numerical variables about a person before deciding on an appropriate rate for automobile insurance. A representative from a local insurance agency selected a random sample of insured drivers and recorded, X, the number of claims each made in the last three years, with the following results.
X f
1 14
2 18
3 12
4 5
5 1
9) Referring to Table 2-1, how many drivers are represented in the sample?
A) 5
B) 15
C) 18
D) 50
Answer: D
Difficulty: Easy
Keywords: frequency distribution
10) Referring to Table 2-1, how many total claims are represented in the sample?
A) 15
B) 50
C) 111
D) 250
Answer: C
Difficulty: Moderate
Keywords: interpretation, frequency distribution
11) A type of vertical bar chart in which the categories are plotted in the descending rank order of the magnitude of their frequencies is called a
A) contingency table.
B) Pareto chart.
C) stem-and-leaf display.
D) pie chart.
Answer: B
Difficulty: Easy
Keywords: Pareto chart
TABLE 2-2
At a meeting of information systems officers for regional offices of a national company, a survey was taken to determine the number of employees the officers supervise in the operation of their departments, where X is the number of employees overseen by each information systems officer.
X f
1 7
2 3
3 11
4 8
5 9
12) Referring to Table 2-2, how many regional offices are represented in the survey results?
A) 5
B) 11
C) 15
D) 40
Answer: D
Difficulty: Easy
Keywords: interpretation, frequency distribution
13) Referring to Table 2-2, across all of the regional offices, how many total employees were supervised by those surveyed?
A) 15
B) 40
C) 127
D) 200
Answer: C
Difficulty: Moderate
Keywords: interpretation, frequency distribution
14) The width of each bar in a histogram corresponds to the
A) differences between the boundaries of the class.
B) number of observations in each class.
C) midpoint of each class.
D) percentage of observations in each class.
Answer: A
Difficulty: Easy
Keywords: frequency distribution
TABLE 2-3
Every spring semester, the School of Business coordinates a luncheon with local business leaders for graduating seniors, their families, and friends. Corporate sponsorship pays for the lunches of each of the seniors, but students have to purchase tickets to cover the cost of lunches served to guests they bring with them. The following histogram represents the attendance at the senior luncheon, where X is the number of guests each graduating senior invited to the luncheon and f is the number of graduating seniors in each category.
15) Referring to the histogram from Table 2-3, how many graduating seniors attended the luncheon?
A) 4
B) 152
C) 275
D) 388
Answer: C
Explanation: C) The number of graduating seniors is the sum of all the frequencies, f.
Difficulty: Difficult
Keywords: interpretation, histogram
16) Referring to the histogram from Table 2-3, if all the tickets purchased were used, how many guests attended the luncheon?
A) 4
B) 152
C) 275
D) 388
Answer: D
Difficulty: Difficult
Keywords: interpretation, histogram
17) A professor of economics at a small Texas university wanted to determine what year in school students were taking his tough economics course. Shown below is a pie chart of the results. What percentage of the class took the course prior to reaching their senior year?
A) 14%
B) 44%
C) 54%
D) 86%
Answer: D
Difficulty: Easy
Keywords: interpretation, pie chart
18) When polygons or histograms are constructed, which axis must show the true zero or "origin"?
A) the horizontal axis
B) the vertical axis
C) both the horizontal and vertical axes
D) neither the horizontal nor the vertical axis
Answer: B
Difficulty: Easy
Keywords: polygon, histogram
19) When constructing charts, the following is plotted at the class midpoints:
A) frequency histograms.
B) percentage polygons.
C) cumulative percentage polygon (ogives).
D) all of the above
Answer: B
Difficulty: Easy
Keywords: percentage polygon
TABLE 2-4
A survey was conducted to determine how people rated the quality of programming available on television. Respondents were asked to rate the overall quality from 0 (no quality at all) to 100 (extremely good quality). The stem-and-leaf display of the data is shown below.
Stem Leaves
3 2 3
4 0 3 4 7 8 9 9 9
5 0 1 1 2 3 4 5
6 1 2 5 6 6
7 0 1
8
9 2
20) Referring to Table 2-4, what percentage of the respondents rated overall television quality with a rating of 80 or above?
A) 0
B) 4
C) 96
D) 100
Answer: B
Difficulty: Easy
Keywords: stem-and-leaf display, interpretation
21) Referring to Table 2-4, what percentage of the respondents rated overall television quality with a rating of 50 or below?
A) 11
B) 40
C) 44
D) 56
Answer: C
Difficulty: Moderate
Keywords: stem-and-leaf display, interpretation
22) Referring to Table 2-4, what percentage of the respondents rated overall television quality with a rating from 50 through 75?
A) 11
B) 40
C) 44
D) 56
Answer: D
Difficulty: Moderate
Keywords: stem-and-leaf display, interpretation
TABLE 2-5
The following are the duration in minutes of a sample of long-distance phone calls made within the continental United States reported by one long-distance carrier.
Relative
Time (in Minutes) Frequency
0 but less than 5 0.37
5 but less than 10 0.22
10 but less than 15 0.15
15 but less than 20 0.10
20 but less than 25 0.07
25 but less than 30 0.07
30 or more 0.02
23) Referring to Table 2-5, what is the width of each class?
A) 1 minute
B) 5 minutes
C) 2%
D) 100%
Answer: B
Difficulty: Easy
Keywords: class interval, relative frequency distribution
24) Referring to Table 2-5, if 1,000 calls were randomly sampled, how many calls lasted under 10 minutes?
A) 220
B) 370
C) 410
D) 590
Answer: D
Difficulty: Moderate
Keywords: relative frequency distribution, interpretation
25) Referring to Table 2-5, if 100 calls were randomly sampled, how many calls lasted 15 minutes or longer?
A) 10
B) 14
C) 26
D) 74
Answer: C
Difficulty: Moderate
Keywords: relative frequency distribution, interpretation
26) Referring to Table 2-5, if 10 calls lasted 30 minutes or more, how many calls lasted less than 5 minutes?
A) 10
B) 185
C) 295
D) 500
Answer: B
Difficulty: Moderate
Keywords: relative frequency distribution, interpretation
27) Referring to Table 2-5, what is the cumulative relative frequency for the percentage of calls that lasted under 20 minutes?
A) 0.10
B) 0.59
C) 0.76
D) 0.84
Answer: D
Difficulty: Easy
Keywords: cumulative relative frequency
28) Referring to Table 2-5, what is the cumulative relative frequency for the percentage of calls that lasted 10 minutes or more?
A) 0.16
B) 0.24
C) 0.41
D) 0.90
Answer: C
Difficulty: Moderate
Keywords: cumulative relative frequency
29) Referring to Table 2-5, if 100 calls were randomly sampled, ________ of them would have lasted at least 15 minutes but less than 20 minutes
A) 6
B) 8
C) 10
D) 16
Answer: C
Difficulty: Easy
Keywords: relative frequency distribution, interpretation
30) Referring to Table 2-5, if 100 calls were sampled, ________ of them would have lasted less than 15 minutes.
A) 26
B) 74
C) 10
D) none of the above
Answer: B
Difficulty: Moderate
Keywords: relative frequency distribution, interpretation
31) Referring to Table 2-5, if 100 calls were sampled, ________ of them would have lasted 20 minutes or more.
A) 26
B) 16
C) 74
D) none of the above
Answer: B
Difficulty: Moderate
Keywords: relative frequency distribution, interpretation
32) Referring to Table 2-5, if 100 calls were sampled, ________ of them would have lasted less than 5 minutes or at least 30 minutes or more.
A) 35
B) 37
C) 39
D) none of the above
Answer: C
Difficulty: Difficult
Keywords: relative frequency distribution, interpretation
33) Which of the following is appropriate for displaying data collected on the different brands of cars that students at a major university drive?
A) a Pareto chart
B) a two-way classification table
C) a histogram
D) a scatter plot
Answer: A
Difficulty: Easy
Keywords: Pareto diagram
34) One of the developing countries is experiencing a baby boom, with the number of births rising for the fifth year in a row, according to a BBC News report. Which of the following is best for displaying this data?
A) a Pareto chart
B) a two-way classification table
C) a histogram
D) a time-series plot
Answer: D
Difficulty: Easy
Keywords: time-series plot
35) When studying the simultaneous responses to two categorical questions, you should set up a
A) contingency table.
B) frequency distribution table.
C) cumulative percentage distribution table.
D) histogram.
Answer: A
Difficulty: Easy
Keywords: contingency table
36) Data on 1,500 students' height were collected at a larger university in the East Coast. Which of the following is the best chart for presenting the information?
A) a pie chart
B) a Pareto chart
C) a side-by-side bar chart
D) a histogram
Answer: D
Difficulty: Easy
Keywords: choice of chart, histogram
37) Data on the number of part-time hours students at a public university worked in a week were collected. Which of the following is the best chart for presenting the information?
A) a pie chart
B) a Pareto chart
C) a percentage table
D) a percentage polygon
Answer: D
Difficulty: Easy
Keywords: choice of chart, percentage polygon
38) Data on the number of credit hours of 20,000 students at a public university enrolled in a spring semester were collected. Which of the following is the best for presenting the information?
A) a pie chart
B) a Pareto chart
C) a stem-and-leaf display
D) a contingency table
Answer: C
Difficulty: Easy
Keywords: choice of chart, stem-and-leaf
39) In a survey, 150 executives were asked what they think is the most common mistake candidates make during job interviews. Six different mistakes were given. Which of the following is the best for presenting the information?
A) a bar chart
B) a histogram
C) a stem-and-leaf display
D) a contingency table
Answer: A
Difficulty: Easy
Keywords: choice of chart, bar chart
40) You have collected information on the market share of five different search engines used by U.S. Internet users in January 2011. Which of the following is the best for presenting the information?
A) a pie chart
B) a histogram
C) a stem-and-leaf display
D) a contingency table
Answer: A
Difficulty: Easy
Keywords: choice of chart, pie chart
41) You have collected information on the consumption by the 15 largest coffee-consuming nations. Which of the following is the best for presenting the shares of the consumption?
A) a pie chart
B) a Pareto chart
C) a side-by-side bar chart
D) a contingency table
Answer: B
Explanation: B) Even though a pie chart can also be used, the Pareto chart is preferable for separating the "vital few" from the "trivial many".
Difficulty: Moderate
Keywords: choice of chart, Pareto chart
42) You have collected data on the approximate retail price (in $) and the energy cost per year (in $) of 15 refrigerators. Which of the following is the best for presenting the data?
A) a pie chart
B) a scatter plot
C) a side-by-side bar chart
D) a contingency table
Answer: B
Difficulty: Easy
Keywords: choice of chart, scatter plot
43) You have collected data on the number of U.S. households actively using online banking and/or online bill payment from 1995 to 2010. Which of the following is the best for presenting the data?
A) a pie chart
B) a stem-and-leaf display
C) a side-by-side bar chart
D) a time-series plot
Answer: D
Difficulty: Easy
Keywords: choice of chart, time-series plot
44) You have collected data on the monthly seasonally adjusted civilian unemployment rate for the United States from 1998 to 2010. Which of the following is the best for presenting the data?
A) a contingency table
B) a stem-and-leaf display
C) a time-series plot
D) a side-by-side bar chart
Answer: D
Difficulty: Easy
Keywords: choice of chart, time-series plot
45) You have collected data on the number of complaints for six different brands of automobiles sold in the United States in 2006 and in 2010. Which of the following is the best for presenting the data?
A) a contingency table
B) a stem-and-leaf display
C) a time-series plot
D) a side-by-side bar chart
Answer: D
Difficulty: Moderate
Keywords: choice of chart, side-by-side bar chart
46) You have collected data on the responses to two questions asked in a survey of 40 college students majoring in business What is your gender (Male = M; Female = F) and What is your major (Accountancy = A; Computer Information Systems = C; Marketing = M). Which of the following is the best for presenting the data?
A) a contingency table
B) a stem-and-leaf display
C) a time-series plot
D) a Pareto chart
Answer: A
Difficulty: Moderate
Keywords: choice of chart, contingency table
TABLE 2-6
A sample of 200 students at a Big Ten university was taken after the midterm to ask them whether they went bar hopping the weekend before the midterm or spent the weekend studying, and whether they did well or poorly on the midterm. The following table contains the result.
| Did Well in Midterm | Did Poorly in Midterm | |
| Studying for Exam | 80 | 20 |
| Went Bar Hopping | 30 | 70 |
47) Referring to Table 2-6, of the students in the sample who went bar hopping the weekend before the midterm, ________ percent did well on the midterm.
A) 15
B) 27.27
C) 30
D) 55
Answer: C
Difficulty: Easy
Keywords: contingency table, interpretation
48) Referring to Table 2-6, of the students in the sample who did well on the midterm, ________ percent went bar hopping the weekend before the midterm.
A) 15
B) 27.27
C) 30
D) 50
Answer: B
Difficulty: Easy
Keywords: contingency table, interpretation
49) Referring to Table 2-6, ________ percent of the students in the sample went bar hopping the weekend before the midterm and did well on the midterm.
A) 15
B) 27.27
C) 30
D) 50
Answer: A
Difficulty: Easy
Keywords: contingency table, interpretation
50) Referring to Table 2-6, ________ percent of the students in the sample spent the weekend studying and did well on the midterm.
A) 40
B) 50
C) 72.72
D) 80
Answer: A
Difficulty: Easy
Keywords: contingency table, interpretation
51) Referring to Table 2-6, if the sample is a good representation of the population, we can expect ________ percent of the students in the population to spend the weekend studying and do poorly on the midterm.
A) 10
B) 20
C) 45
D) 50
Answer: A
Difficulty: Easy
Keywords: contingency table, interpretation
52) Referring to Table 2-6, if the sample is a good representation of the population, we can expect ________ percent of those who spent the weekend studying to do poorly on the midterm.
A) 10
B) 20
C) 45
D) 50
Answer: B
Difficulty: Moderate
Keywords: contingency table, interpretation
53) Referring to Table 2-6, if the sample is a good representation of the population, we can expect ________ percent of those who did poorly on the midterm to have spent the weekend studying.
A) 10
B) 22.22
C) 45
D) 50
Answer: B
Difficulty: Moderate
Keywords: contingency table, interpretation
54) In a contingency table, the number of rows and columns
A) must always be the same.
B) must always be 2.
C) must add to 100%.
D) none of the above
Answer: D
Difficulty: Moderate
Keywords: contingency table
55) Retailers are always interested in determining why a customer selected their store to make a purchase. A sporting goods retailer conducted a customer survey to determine why its customers shopped at the store. The results are shown in the bar chart below. What proportion of the customers responded that they shopped at the store because of the merchandise or the convenience?
A) 35%
B) 50%
C) 65%
D) 85%
Answer: C
Difficulty: Easy
Keywords: bar chart, interpretation
TABLE 2-7
The stem-and-leaf display below contains data on the number of months between the date a civil suit is filed and when the case is actually adjudicated for 50 cases heard in superior court.
Stem Leaves
1 2 3 4 4 4 7 8 9 9
2 2 2 2 2 3 4 5 5 6 7 8 8 8 9
3 0 0 1 1 1 3 5 7 7 8
4 0 2 3 4 5 5 7 9
5 1 1 2 4 6 6
6 1 5 8
56) Referring to Table 2-7, locate the first leaf, i.e., the lowest valued leaf with the lowest valued stem. This represents a wait of ________ months.
Answer: 12
Difficulty: Easy
Keywords: stem-and-leaf display, interpretation
57) Referring to Table 2-7, the civil suit with the longest wait between when the suit was filed and when it was adjudicated had a wait of ________ months.
Answer: 68
Difficulty: Easy
Keywords: stem-and-leaf display, interpretation
58) Referring to Table 2-7, the civil suit with the fourth shortest waiting time between when the suit was filed and when it was adjudicated had a wait of ________ months.
Answer: 14
Difficulty: Moderate
Keywords: stem-and-leaf display, interpretation
59) Referring to Table 2-7, ________ percent of the cases were adjudicated within the first two years.
Answer: 30
Difficulty: Moderate
Keywords: stem-and-leaf display, interpretation
60) Referring to Table 2-7, ________ percent of the cases were not adjudicated within the first four years.
Answer: 20
Difficulty: Moderate
Keywords: stem-and-leaf display, interpretation
61) Referring to Table 2-7, if a frequency distribution with equal sized classes was made from this data, and the first class was "10 but less than 20," the frequency of that class would be ________.
Answer: 9
Difficulty: Easy
Keywords: stem-and-leaf display, interpretation
62) Referring to Table 2-7, if a frequency distribution with equal sized classes was made from this data, and the first class was "10 but less than 20," the relative frequency of the third class would be ________.
Answer: 0.20 or 20% or 10/50
Difficulty: Moderate
Keywords: stem-and-leaf display, relative frequency distribution
63) Referring to Table 2-7, if a frequency distribution with equal sized classes was made from this data, and the first class was "10 but less than 20," the cumulative percentage of the second class would be ________.
Answer: 46% or 0.46 or 23/50
Difficulty: Moderate
Keywords: stem-and-leaf display, cumulative percentage distribution
TABLE 2-8
The stem-and-leaf display represents the number of times in a year that a random sample of 100 "lifetime" members of a health club actually visited the facility.
Stem Leaves
0 012222233333344566666667789999
1 1111222234444455669999
2 00011223455556889
3 0000446799
4 011345567
5 0077
6 8
7 67
8 3
9 0247
64) Referring to Table 2-8, the person who has the largest leaf associated with the smallest stem visited the facility ________ times.
Answer: 9
Difficulty: Moderate
Keywords: stem-and-leaf display, interpretation
65) Referring to Table 2-8, the person who visited the health club less than anyone else in the sample visited the facility ________ times.
Answer: 0 or no
Difficulty: Easy
Keywords: stem-and-leaf display, interpretation
66) Referring to Table 2-8, the person who visited the health club more than anyone else in the sample visited the facility ________ times.
Answer: 97
Difficulty: Easy
Keywords: stem-and-leaf display, interpretation
67) Referring to Table 2-8, ________ of the 100 members visited the health club at least 52 times in a year.
Answer: 10
Difficulty: Moderate
Keywords: stem-and-leaf display, interpretation
68) Referring to Table 2-8, ________ of the 100 members visited the health club no more than 12 times in a year.
Answer: 38
Difficulty: Moderate
Keywords: stem-and-leaf display, interpretation
69) Referring to Table 2-8, if a frequency distribution with equal sized classes was made from this data, and the first class was "0 but less than 10," the frequency of the fifth class would be ________.
Answer: 9
Difficulty: Moderate
Keywords: stem-and-leaf display, frequency distribution
70) Referring to Table 2-8, if a frequency distribution with equal sized classes was made from this data, and the first class was "0 but less than 10," the relative frequency of the last class would be ________.
Answer: 4% or 0.04 or 4/100
Difficulty: Moderate
Keywords: stem-and-leaf display, relative frequency distribution
71) Referring to Table 2-8, if a frequency distribution with equal sized classes was made from this data, and the first class was "0 but less than 10," the cumulative percentage of the next-to-last class would be ________.
Answer: 96% or 0.96 or 96/100
Difficulty: Moderate
Keywords: stem-and-leaf display, cumulative percentage distribution
72) Referring to Table 2-8, if a frequency distribution with equal sized classes was made from this data, and the first class was "0 but less than 10," the class midpoint of the third class would be ________.
Answer: 25 or (20+30)/2
Difficulty: Moderate
Keywords: stem-and-leaf display, class midpoint
TABLE 2-9
The frequency distribution below represents the rents of 250 randomly selected federally subsidized apartments in a small town.
Rent in $ Frequency
300 but less than 400 113
400 but less than 500 85
500 but less than 600 32
600 but less than 700 16
700 but less than 800 4
73) Referring to Table 2-9, ________ apartments rented for at least $400 but less than $600.
Answer: 117
Difficulty: Easy
Keywords: frequency distribution
74) Referring to Table 2-9, ________ percent of the apartments rented for $600 or more.
Answer: 8 or 20/250
Difficulty: Easy
Keywords: frequency distribution, cumulative percentage distribution
75) Referring to Table 2-9, ________ percent of the apartments rented for at least $500.
Answer: 20.8 or 52/250
Difficulty: Moderate
Keywords: frequency distribution, cumulative percentage distribution
76) Referring to Table 2-9, the class midpoint of the second class is ________.
Answer: 450
Difficulty: Easy
Keywords: frequency distribution, class midpoint
77) Referring to Table 2-9, the relative frequency of the second class is ________.
Answer: 85/250 or 17/50 or 34% or 0.34
Difficulty: Easy
Keywords: frequency distribution, relative frequency distribution
78) Referring to Table 2-9, the percentage of apartments renting for less than $600 is ________.
Answer: 230/250 or 23/25 or 92% or 0.92
Difficulty: Moderate
Keywords: frequency distribution, cumulative percentage distribution
TABLE 2-10
The histogram below represents scores achieved by 200 job applicants on a personality profile.
79) Referring to the histogram from Table 2-10, ________ percent of the job applicants scored between 10 and 20.
Answer: 20
Difficulty: Easy
Keywords: histogram, percentage distribution
80) Referring to the histogram from Table 2-10, ________ percent of the job applicants scored below 50.
Answer: 80
Difficulty: Moderate
Keywords: histogram, percentage distribution
81) Referring to the histogram from Table 2-10, the number of job applicants who scored between 30 and below 60 is ________.
Answer: 80
Difficulty: Moderate
Keywords: histogram
82) Referring to the histogram from Table 2-10, the number of job applicants who scored 50 or above is ________.
Answer: 40
Difficulty: Moderate
Keywords: histogram
83) Referring to the histogram from Table 2-10, 90% of the job applicants scored above or equal to ________.
Answer: 10
Difficulty: Moderate
Keywords: histogram, cumulative percentage distribution
84) Referring to the histogram from Table 2-10, half of the job applicants scored below ________.
Answer: 30
Difficulty: Moderate
Keywords: histogram, cumulative percentage distribution
85) Referring to the histogram from Table 2-10, ________ percent of the applicants scored below 20 or at least 50.
Answer: 50
Difficulty: Moderate
Keywords: histogram, cumulative percentage distribution
86) Referring to the histogram from Table 2-10, ________ percent of the applicants scored between 20 and below 50.
Answer: 50
Difficulty: Moderate
Keywords: histogram, cumulative percentage distribution
TABLE 2-11
The ordered array below resulted from selecting a sample of 25 batches of 500 computer chips and determining how many in each batch were defective.
Defects
1 2 4 4 5 5 6 7 9 9 12 12 15
17 20 21 23 23 25 26 27 27 28 29 29
87) Referring to Table 2-11, if a frequency distribution for the defects data is constructed, using "0 but less than 5" as the first class, the frequency of the "20 but less than 25" class would be ________.
Answer: 4
Difficulty: Easy
Keywords: frequency distribution
88) Referring to Table 2-11, if a frequency distribution for the defects data is constructed, using "0 but less than 5" as the first class, the relative frequency of the "15 but less than 20" class would be ________.
Answer: 0.08 or 8% or 2/25
Difficulty: Moderate
Keywords: relative frequency distribution
89) Referring to Table 2-11, construct a frequency distribution for the defects data, using "0 but less than 5" as the first class.
Answer: Defects Frequency
0 but less than 5 4
5 but less than 10 6
10 but less than 15 2
15 but less than 20 2
20 but less than 25 4
25 but less than 30 7
Difficulty: Easy
Keywords: frequency distribution
90) Referring to Table 2-11, construct a relative frequency or percentage distribution for the defects data, using "0 but less than 5" as the first class.
Answer: Defects Percentage
0 but less than 5 16
5 but less than 10 24
10 but less than 15 8
15 but less than 20 8
20 but less than 25 16
25 but less than 30 28
Difficulty: Moderate
Keywords: relative frequency distribution, percentage distribution
91) Referring to Table 2-11, construct a cumulative percentage distribution for the defects data if the corresponding frequency distribution uses "0 but less than 5" as the first class.
Answer: Defects CumPct
0 0
5 16
10 40
15 48
20 56
25 72
30 100
Difficulty: Moderate
Keywords: cumulative percentage distribution
92) Referring to Table 2-11, construct a histogram for the defects data, using "0 but less than 5" as the first class.
Answer:
Difficulty: Easy
Keywords: histogram, frequency distribution
93) Referring to Table 2-11, construct a cumulative percentage polygon for the defects data if the corresponding frequency distribution uses "0 but less than 5" as the first class.
Answer:
Difficulty: Moderate
Keywords: cumulative percentage polygon
94) The point halfway between the boundaries of each class interval in a grouped frequency distribution is called the ________.
Answer: class midpoint
Difficulty: Easy
Keywords: cumulative percentage polygon, frequency distribution
95) A ________ is a vertical bar chart in which the rectangular bars are constructed at the boundaries of each class interval.
Answer: histogram
Difficulty: Easy
Keywords: histogram
96) It is essential that each class grouping or interval in a frequency distribution be ________ and ________.
Answer: non-overlapping and of equal width
Difficulty: Moderate
Keywords: frequency distribution, class interval
97) In order to compare one large set of numerical data to another, a ________ distribution must be developed from the frequency distribution.
Answer: relative frequency or percentage
Difficulty: Easy
Keywords: relative frequency distribution, percentage distribution
98) When comparing two or more large sets of numerical data, the distributions being developed should use the same ________.
Answer: class boundaries.
Difficulty: Easy
Keywords: class boundaries
99) The width of each class grouping or interval in a frequency distribution should be ________.
Answer: the same or equal
Difficulty: Easy
Keywords: class interval, frequency distribution
100) In constructing a polygon, each class grouping is represented by its ________ and then these are consecutively connected to one another.
Answer: midpoint
Difficulty: Easy
Keywords: polygon, class interval, midpoint
101) A ________ is a summary table in which numerical data are tallied into class intervals or categories.
Answer: frequency distribution
Difficulty: Easy
Keywords: frequency distribution, class interval
102) True or False: In general, grouped frequency distributions should have between 5 and 15 class intervals.
Answer: TRUE
Difficulty: Easy
Keywords: frequency distribution, number of classes
103) True or False: The sum of relative frequencies in a distribution always equals 1.
Answer: TRUE
Difficulty: Easy
Keywords: relative frequency
104) True or False: The sum of cumulative frequencies in a distribution always equals 1.
Answer: FALSE
Difficulty: Moderate
Keywords: cumulative distribution
105) True or False: In graphing two categorical data, the side-by-side bar chart is best suited when comparing joint responses.
Answer: TRUE
Difficulty: Moderate
Keywords: side-by-side chart
106) True or False: When constructing a frequency distribution, classes should be selected so that they are of equal width.
Answer: TRUE
Difficulty: Easy
Keywords: frequency distribution
107) True or False: A research analyst was directed to arrange raw data collected on the yield of wheat, ranging from 40 to 93 bushels per acre, in a frequency distribution. He should choose 30 as the class interval width.
Answer: FALSE
Difficulty: Easy
Keywords: frequency distribution, class interval
108) True or False: If the values of the seventh and eighth class in a cumulative percentage distribution are the same, we know that there are no observations in the eighth class.
Answer: TRUE
Difficulty: Moderate
Keywords: cumulative percentage distribution
109) True or False: One of the advantages of a pie chart is that it clearly shows that the total of all the categories of the pie adds to 100%.
Answer: TRUE
Difficulty: Easy
Keywords: pie chart
110) True or False: The larger the number of observations in a numerical data set, the larger the number of class intervals needed for a grouped frequency distribution.
Answer: TRUE
Difficulty: Easy
Keywords: class interval, frequency distribution
111) True or False: Determining the class boundaries of a frequency distribution is highly subjective.
Answer: TRUE
Difficulty: Easy
Keywords: class boundaries, frequency distribution
112) True or False: The original data values cannot be determined once they are grouped into a frequency distribution table.
Answer: TRUE
Difficulty: Easy
Keywords: frequency distribution
113) True or False: The percentage distribution cannot be constructed from the frequency distribution directly.
Answer: FALSE
Difficulty: Easy
Keywords: percentage distribution, frequency distribution
114) True or False: The stem-and-leaf display is often superior to the frequency distribution in that it maintains the original values for further analysis.
Answer: TRUE
Difficulty: Easy
Keywords: stem-and-leaf display, frequency distribution
115) True or False: The relative frequency is the frequency in each class divided by the total number of observations.
Answer: TRUE
Difficulty: Easy
Keywords: relative frequency distribution
116) True or False: Ogives are plotted at the midpoints of the class groupings.
Answer: FALSE
Difficulty: Easy
Keywords: ogives, midpoint
117) True or False: Percentage polygons are plotted at the boundaries of the class groupings.
Answer: FALSE
Difficulty: Easy
Keywords: percentage polygons
118) True or False: The main principle behind the Pareto chart is the ability to separate the "vital few" from the "trivial many."
Answer: TRUE
Difficulty: Easy
Keywords: Pareto chart
119) True or False: A histogram can have gaps between the bars, whereas bar charts cannot have gaps.
Answer: FALSE
Difficulty: Easy
Keywords: histogram, bar chart
120) True or False: Histograms are used for numerical data while bar charts are suitable for categorical data.
Answer: TRUE
Difficulty: Easy
Keywords: histogram, bar chart
121) True or False: A Walmart store in a small town monitors customer complaints and organizes these complaints into six distinct categories. Over the past year, the company has received 534 complaints. One possible graphical method for representing these data would be a Pareto chart.
Answer: TRUE
Difficulty: Moderate
Keywords: Pareto chart
122) True or False: Apple Computer, Inc. collected information on the age of its customers. The youngest customer was 12 and the oldest was 72. To study the distribution of the age among its customers, it can use a Pareto chart.
Answer: FALSE
Difficulty: Moderate
Keywords: Pareto chart
123) True or False: Apple Computer, Inc. collected information on the age of its customers. The youngest customer was 12 and the oldest was 72. To study the distribution of the age among its customers, it is best to use a pie chart.
Answer: FALSE
Difficulty: Moderate
Keywords: pie chart
124) True or False: Apple Computer, Inc. collected information on the age of its customers. The youngest customer was 12 and the oldest was 72. To study the distribution of the age among its customers, it can use a percentage polygon.
Answer: TRUE
Difficulty: Moderate
Keywords: percentage polygon
125) True or False: Apple Computer, Inc. collected information on the age of its customers. The youngest customer was 12 and the oldest was 72. To study the percentage of their customers who are below a certain age, it can use an ogive.
Answer: TRUE
Difficulty: Moderate
Keywords: ogive
126) True or False: If you wish to construct a graph of a relative frequency distribution, you would most likely construct an ogive first.
Answer: FALSE
Difficulty: Moderate
Keywords: Ogive
127) True or False: An ogive is a cumulative percentage polygon.
Answer: TRUE
Difficulty: Easy
Keywords: Ogive, cumulative percentage polygon
128) True or False: A side-by-side chart is two histograms plotted side-by-side.
Answer: FALSE
Difficulty: Moderate
Keywords: side-by-side chart
129) True or False: A good choice for the number of class groups to use in constructing frequency distribution is to have at least 5 but no more than 15 class groups.
Answer: TRUE
Difficulty: Easy
Keywords: number of classes
130) True or False: In general, a frequency distribution should have at least 8 class groups but no more than 20.
Answer: FALSE
Difficulty: Easy
Keywords: number of classes
131) True or False: True of False: To determine the width of class interval, divide the number of class groups by the range of the data.
Answer: FALSE
Difficulty: Easy
Keywords: class interval
132) True or False: The percentage polygon is formed by having the lower boundary of each class represent the data in that class and then connecting the sequence of lower boundaries at their respective class percentages.
Answer: FALSE
Difficulty: Easy
Keywords: percentage polygon
133) True or False: A polygon can be constructed from a bar chart.
Answer: FALSE
Difficulty: Moderate
Keywords: polygon
134) True or False: To evaluate two categorical variables at the same time, a ________ could be developed.
Answer: contingency or cross-classification table or side-by-side bar chart
Difficulty: Easy
Keywords: contingency table, cross-classification table
135) True or False: Relationships in a contingency table can be examined more fully if the frequencies are converted into ________.
Answer: percentages or proportions
Difficulty: Easy
Keywords: contingency table
TABLE 2-12
The table below contains the opinions of a sample of 200 people broken down by gender about the latest congressional plan to eliminate anti-trust exemptions for professional baseball.
For Neutral Against Totals
Female 38 54 12 104
Male 12 36 48 96
Totals 50 90 60 200
136) Referring to Table 2-12, construct a table of row percentages.
Answer: For Neutral Against Totals
Female 36.54 51.92 11.54 100.00
Male 2.50 37.50 50.00 100.00
Totals 25.00 45.00 30.00 100.00
Difficulty: Easy
Keywords: row percentages
137) Referring to Table 2-12, construct a table of column percentages.
Answer: For Neutral Against Totals
Female 76.00 60.00 20.00 52.00
Male 24.00 40.00 80.00 48.00
Totals 100.00 100.00 100.00 100.00
Difficulty: Easy
Keywords: column percentages
138) Referring to Table 2-12, construct a table of total percentages.
Answer: For Neutral Against Totals
Female 19.00 27.00 6.00 52.00
Male 6.00 18.00 24.00 48.00
Totals 25.00 45.00 30.00 100.00
Difficulty: Easy
Keywords: total percentages
139) Referring to Table 2-12, of those for the plan in the sample, ________ percent were females.
Answer: 76
Difficulty: Moderate
Keywords: contingency table, column percentages
140) Referring to Table 2-12, of those neutral in the sample, ________ percent were males.
Answer: 40
Difficulty: Moderate
Keywords: contingency table, column percentages
141) Referring to Table 2-12, of the males in the sample, ________ percent were for the plan.
Answer: 12.50
Difficulty: Moderate
Keywords: contingency table
142) Referring to Table 2-12, of the females in the sample, ________ percent were against the plan.
Answer: 11.54
Difficulty: Moderate
Keywords: contingency table
143) Referring to Table 2-12, of the females in the sample, ________ percent were either neutral or against the plan.
Answer: 63.46 or (51.92+11.54)
Difficulty: Moderate
Keywords: contingency table
144) Referring to Table 2-12, ________ percent of the 200 were females who were against the plan.
Answer: 6
Difficulty: Moderate
Keywords: contingency table
145) Referring to Table 2-12, ________ percent of the 200 were males who were neutral.
Answer: 18
Difficulty: Moderate
Keywords: contingency table
146) Referring to Table 2-12, ________ percent of the 200 were females who were either neutral or against the plan.
Answer: 33
Difficulty: Difficult
Keywords: contingency table
147) Referring to Table 2-12, ________ percent of the 200 were males who were not against the plan.
Answer: 24
Difficulty: Difficult
Keywords: contingency table
148) Referring to Table 2-12, ________ percent of the 200 were not neutral.
Answer: 55
Difficulty: Difficult
Keywords: contingency table, row percentages
149) Referring to Table 2-12, ________ percent of the 200 were against the plan.
Answer: 30
Difficulty: Moderate
Keywords: contingency table, row percentages
150) Referring to Table 2-12, ________ percent of the 200 were males.
Answer: 48
Difficulty: Easy
Keywords: contingency table, column percentages
151) Referring to Table 2-12, if the sample is a good representation of the population, we can expect ________ percent of the population will be for the plan.
Answer: 25
Difficulty: Moderate
Keywords: contingency table, row percentages
152) Referring to Table 2-12, if the sample is a good representation of the population, we can expect ________ percent of the population will be males.
Answer: 48
Difficulty: Moderate
Keywords: contingency table, column percentages
153) Referring to Table 2-12, if the sample is a good representation of the population, we can expect ________ percent of those for the plan in the population will be males.
Answer: 24
Difficulty: Moderate
Keywords: contingency table
154) Referring to Table 2-12, if the sample is a good representation of the population, we can expect ________ percent of the males in the population will be against the plan.
Answer: 50
Difficulty: Moderate
Keywords: contingency table
155) Referring to Table 2-12, if the sample is a good representation of the population, we can expect ________ percent of the females in the population will not be against the plan.
Answer: 88.46 or (36.54+51.92)
Difficulty: Moderate
Keywords: contingency table
TABLE 2-13
Given below is the stem-and-leaf display representing the amount of detergent used in gallons (with leaves in tenths of gallons) in a day by 25 drive-through car wash operations in Phoenix.
9 | 147
10 | 02238
11 | 135566777
12 | 223489
13 | 02
156) Referring to Table 2-13, if a frequency distribution for the amount of detergent used is constructed, using "9.0 but less than 10.0 gallons" as the first class, the frequency of the "11.0 but less than 12.0 gallons" class would be ________.
Answer: 9
Difficulty: Easy
Keywords: frequency distribution
157) Referring to Table 2-13, if a percentage histogram for the detergent data is constructed, using "9.0 but less than 10.0 gallons" as the first class, the percentage of drive-through car wash operations that use "12.0 but less than 13.0 gallons" of detergent would be ________.
Answer: 24%
Difficulty: Moderate
Keywords: relative frequency distribution, percentage distribution
158) Referring to Table 2-13, if a percentage histogram for the detergent data is constructed, using "9.0 but less than 10.0 gallons" as the first class, what percentage of drive-through car wash operations use less than 12 gallons of detergent in a day?
Answer: 68%
Difficulty: Easy
Keywords: percentage distribution, cumulative relative frequency
159) Referring to Table 2-13, if a relative frequency or percentage distribution for the detergent data is constructed, using "9.0 but less than 10.0 gallons" as the first class, what percentage of drive-through car wash operations use at least 10 gallons of detergent in a day?
Answer: 88%
Difficulty: Easy
Keywords: relative frequency distribution, percentage distribution
160) Referring to Table 2-13, if a relative frequency or percentage distribution for the detergent data is constructed, using "9.0 but less than 10.0 gallons" as the first class, what percentage of drive-through car wash operations use at least 10 gallons but less than 13 gallons of detergent in a day?
Answer: 80%
Difficulty: Easy
Keywords: relative frequency distribution, percentage distribution
161) Referring to Table 2-13, construct a frequency distribution for the detergent data, using "9.0 but less than 10.0 gallons" as the first class.
Answer:
Purchases (gals) Frequency
9.0 but less than 10.0 3
10.0 but less than 11.0 5
11.0 but less than 12.0 9
12.0 but less than 13.0 6
13.0 but less than 14.0 2
Difficulty: Moderate
Keywords: frequency distribution
162) Referring to Table 2-13, construct a relative frequency or percentage distribution for the detergent data, using "9.0 but less than 10.0" as the first class.
Answer:
Gasoline
Purchases (gals) Percentage
9.0 but less than 10.0 12%
10.0 but less than 11.0 20
11.0 but less than 12.0 36
12.0 but less than 13.0 24
13.0 but less than 14.0 8
Difficulty: Moderate
Keywords: relative frequency distribution, percentage distribution
163) Referring to Table 2-13, construct a cumulative percentage distribution for the detergent data if the corresponding frequency distribution uses "9.0 but less than 10.0" as the first class.
Answer:
Gasoline Frequency Percentage
Purchases (gals) Less Than Less Than
9.0 but less than 10.0 3 12
10.0 but less than 11.0 8 32
11.0 but less than 12.0 17 68
12.0 but less than 13.0 23 92
13.0 but less than 14.0 25 100
Difficulty: Moderate
Keywords: cumulative percentage distribution
164) Referring to Table 2-13, construct a percentage histogram for the detergent data, using "9.0 but less than 10.0" as the first class.
Answer:
Difficulty: Moderate
Keywords: histogram, frequency distribution
165) Referring to Table 2-13, construct a cumulative percentage polygon for the detergent data if the corresponding frequency distribution uses "9.0 but less than 10.0" as the first class.
Answer:
Difficulty: Moderate
Keywords: cumulative percentage polygon
166) Referring to Table 2-13, construct a percentage polygon for the detergent data if the corresponding frequency distribution uses "9.0 but less than 10.0" as the first class.
Answer:
Difficulty: Moderate
Keywords: percentage distribution, percentage polygon
TABLE 2-14
The table below contains the number of people who own a portable DVD player in a sample of 600 broken down by gender.
Own a Portable
DVD Player Male Female
Yes 96 40
No 224 240
167) Referring to Table 2-14, construct a table of row percentages.
Answer:
| Own | Male | Female | Total |
| Yes | 70.59% | 29.41% | 100.00% |
| No | 48.28% | 51.72% | 100.00% |
| Total | 53.33% | 46.67% | 100.00% |
Difficulty: Easy
Keywords: row percentages
168) Referring to Table 2-14, construct a table of column percentages.
Answer:
| Own | Male | Female | Total |
| Yes | 30.00% | 14.29% | 22.67% |
| No | 70.00% | 85.71% | 77.33% |
| Total | 100.00% | 100.00% | 100.00% |
Difficulty: Easy
Keywords: column percentages
169) Referring to Table 2-14, construct a table of total percentages.
Answer:
| Own | Male | Female | Total |
| Yes | 16.00% | 6.67% | 22.67% |
| No | 37.33% | 40.00% | 77.33% |
| Total | 53.33% | 46.67% | 100.00% |
Difficulty: Easy
Keywords: total percentages
170) Referring to Table 2-14, of those who owned a portable DVD in the sample, ________ percent were females.
Answer: 29.41
Difficulty: Moderate
Keywords: contingency table, row percentages
171) Referring to Table 2-14, of those who did not own a portable DVD in the sample, ________ percent were males.
Answer: 48.28
Difficulty: Moderate
Keywords: contingency table, row percentages
172) Referring to Table 2-14, of the males in the sample, ________ percent owned a portable DVD.
Answer: 30
Difficulty: Moderate
Keywords: contingency table, column percentages
173) Referring to Table 2-14, of the females in the sample, ________ percent did not own a portable DVD.
Answer: 85.71
Difficulty: Moderate
Keywords: contingency table, column percentages
174) Referring to Table 2-14 of the females in the sample, ________ percent owned a portable DVD.
Answer: 14.29
Difficulty: Moderate
Keywords: contingency table, column percentages
175) Referring to Table 2-14, ________ percent of the 600 were females who owned a portable DVD.
Answer: 6.67
Difficulty: Moderate
Keywords: contingency table, total percentage
176) Referring to Table 2-14, ________ percent of the 600 were males who owned a portable DVD.
Answer: 16
Difficulty: Moderate
Keywords: contingency table, total percentage
177) Referring to Table 2-14, ________ percent of the 600 were females who either owned or did not own a portable DVD.
Answer: 46.67
Difficulty: Moderate
Keywords: contingency table, total percentage
178) Referring to Table 2-14, ________ percent of the 600 were males who did not own a portable DVD.
Answer: 37.33
Difficulty: Moderate
Keywords: contingency table, total percentage
179) Referring to Table 2-14, ________ percent of the 600 owned a portable DVD.
Answer: 22.67
Difficulty: Moderate
Keywords: contingency table, column percentages
180) Referring to Table 2-14, ________ percent of the 600 did not own a portable DVD.
Answer: 77.33
Difficulty: Moderate
Keywords: contingency table, column percentages
181) Referring to Table 2-14, ________ percent of the 600 were females.
Answer: 46.67
Difficulty: Easy
Keywords: contingency table, row percentages
182) Referring to Table 2-14, if the sample is a good representation of the population, we can expect ________ percent of the population will own a portable DVD.
Answer: 22.67
Difficulty: Moderate
Keywords: contingency table, column percentages
183) Referring to Table 2-14, if the sample is a good representation of the population, we can expect ________ percent of the population will be males.
Answer: 53.33
Difficulty: Moderate
Keywords: contingency table, column percentages
184) Referring to Table 2-14, if the sample is a good representation of the population, we can expect ________ percent of those who own a portable DVD in the population will be males.
Answer: 70.59
Difficulty: Moderate
Keywords: contingency table, row percentages
185) Referring to Table 2-14, if the sample is a good representation of the population, we can expect ________ percent of the males in the population will own a portable DVD.
Answer: 30
Difficulty: Moderate
Keywords: contingency table, column percentages
186) Referring to Table 2-14, if the sample is a good representation of the population, we can expect ________ percent of the females in the population will not own a portable DVD.
Answer: 85.71
Difficulty: Moderate
Keywords: contingency table, column percentages
TABLE 2-15
The figure below is the ogive for the amount of fat (in grams) for a sample of 36 pizza products where the upper boundaries of the intervals are: 5, 10, 15, 20, 25, and 30.
187) Referring to Table 2-15, roughly what percentage of pizza products contain less than 10 grams of fat?
A) 3%
B) 14%
C) 50%
D) 75%
Answer: B
Difficulty: Easy
Keywords: cumulative percentage polygon, ogive, interpretation
188) Referring to Table 2-15, what percentage of pizza products contain at least 20 grams of fat?
A) 5%
B) 25%
C) 75%
D) 96%
Answer: B
Difficulty: Easy
Keywords: cumulative percentage polygon, ogive, interpretation
189) Referring to Table 2-15, what percentage of pizza products contain between 10 and 25 grams of fat?
A) 14%
B) 44%
C) 62%
D) 81%
Answer: D
Difficulty: Easy
Keywords: cumulative percentage polygon, ogive, interpretation
TABLE 2-16
The figure below is the percentage polygon for the amount of calories for a sample of 36 pizzas products where the upper limits of the intervals are: 310, 340, 370, 400 and 430.
190) Referring to Table 2-16, roughly what percentage of pizza products contain between 400 and 430 calories?
A) 0%
B) 11%
C) 89%
D) 100%
Answer: B
Difficulty: Easy
Keywords: percentage polygon, interpretation
191) Referring to Table 2-16, roughly what percentage of pizza products contain between 340 and 400 calories?
A) 22%
B) 25%
C) 28%
D) 50%
Answer: D
Difficulty: Moderate
Keywords: percentage polygon, interpretation
192) Referring to Table 2-16, roughly what percentage of pizza products contain at least 340 calories?
A) 25%
B) 28%
C) 39%
D) 61%
Answer: D
Difficulty: Moderate
Keywords: percentage polygon, interpretation
TABLE 2-17
The following table presents total retail sales in millions of dollars for the leading apparel companies during April 2009 and April 2010.
| Apparel Company | April 2009 | April 2010 |
| Gap | 1,159.00 | 962 |
| TJX | 781.7 | 899 |
| Limited | 596.5 | 620.4 |
| Kohl's | 544.9 | 678.9 |
| Nordstrom | 402.6 | 418.3 |
| Talbots | 139.9 | 130.1 |
| AnnTaylor | 114.2 | 124.8 |
193) Referring to Table 2-17, construct a table of column percentages.
Answer:
| Apparel Company | April 2009 | April 2010 |
| Gap | 31.00% | 25.09% |
| TJX | 20.91% | 23.45% |
| Limited | 15.95% | 16.18% |
| Kohl's | 14.57% | 17.71% |
| Nordstrom | 10.77% | 10.91% |
| Talbots | 3.74% | 3.39% |
| AnnTaylor | 3.05% | 3.26% |
| Total | 100.00% | 100.00% |
Difficulty: Moderate
Keywords: column percentages
194) Referring to Table 2-17, construct a side-by-side bar chart.
Answer:
Difficulty: Moderate
Keywords: column percentages, side-by-side chart
195) True or False: Referring to Table 2-17, in general, retail sales for the apparel industry have seen a modest growth between April 2008 and April 2009.
Answer: TRUE
Difficulty: Easy
Keywords: column percentages, side-by-side chart, interpretation
196) Referring to Table 2-17, among the 8 stores, ________ saw a sales decline.
Answer: Gap and Talbots
Difficulty: Easy
Keywords: column percentages, side-by-side chart, interpretation
TABLE 2-18
The stem-and-leaf display below shows the result of a survey on 50 students on their satisfaction with their school with the higher scores represent higher level of satisfaction.
197) Referring to Table 2-18, what was the highest level of satisfaction?
Answer: 97
Difficulty: Easy
Keywords: stem-and-leaf display
198) Referring to Table 2-18, what was the lowest level of satisfaction?
Answer: 41
Difficulty: Easy
Keywords: stem-and-leaf display
199) Referring to Table 2-18, how many students have a satisfaction level in the 50s?
Answer: 5
Difficulty: Easy
Keywords: stem-and-leaf display
200) Referring to Table 2-18, how many students have a satisfaction level below 60?
Answer: 10
Difficulty: Easy
Keywords: stem-and-leaf display
201) Referring to Table 2-18, how many students have a satisfaction level of at least 80?
Answer: 15
Difficulty: Easy
Keywords: stem-and-leaf display
202) True or False: Referring to Table 2-18, the level of satisfaction is concentrated around 75.
Answer: TRUE
Difficulty: Easy
Keywords: stem-and-leaf display
203) True or False: Referring to Table 2-18, if a student is randomly selected, his/her most likely level of satisfaction among the 40s, 50s, 60s, 70s, 80s and 90s will be in the 70s.
Answer: TRUE
Difficulty: Easy
Keywords: stem-and-leaf display
204) True or False: Referring to Table 2-18, if a student is randomly selected, his/her most likely level of satisfaction among the 40s, 50s, 60s, 70s, 80s and 90s will be in the 60s.
Answer: FALSE
Difficulty: Easy
Keywords: stem-and-leaf display
205) True or False: Given below is the scatter plot of the price/earnings ratio versus earnings per share of 20 U.S. companies. There appears to be a negative relationship between price/earnings ratio and earnings per share.
Answer: TRUE
Difficulty: Easy
Keywords: scatter plot
206) True or False: Given below is the scatter plot of the price/earnings ratio versus earnings per share of 20 U.S. companies. There appear to be a positive relationship between price/earnings ratio and earnings per share.
Answer: FALSE
Difficulty: Moderate
Keywords: scatter plot
207) True or False: Given below is the scatter plot of the market value (thousands$) and profit (thousands$) of 50 U.S. companies. Higher market values appear to be associated with higher profits.
Answer: TRUE
Difficulty: Easy
Keywords: scatter plot
208) True or False: Given below is the scatter plot of the market value (thousands$) and profit (thousands$) of 50 U.S. companies. There appears to be a negative relationship between market value and profit.
Answer: FALSE
Difficulty: Easy
Keywords: scatter plot
209) True or False: Given below is the scatter plot of the number of employees and the total revenue ($millions) of 20 U.S. companies. There appears to be a positive relationship between total revenue and the number of employees.
Answer: TRUE
Difficulty: Moderate
Keywords: scatter plot
210) True or False: Given below is the scatter plot of the number of employees and the total revenue ($millions) of 20 U.S. companies. Companies that have higher numbers of employees appear to also have higher total revenue.
Answer: TRUE
Difficulty: Moderate
Keywords: scatter plot









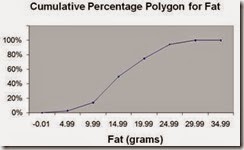


![clip_image028[1] clip_image028[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiS511b8lE44Lmi7QvcdYH25mkUj0jfGcc1h1ptrwvRJnhKX8CroxUwJDwb3UR8Zo9PbV3YvTsxLI2g74WZhzV9Ipep69XAiiQkjm7UwiV0u67AbJLKuv1eH239OgMKs0XFDxei19Al4Xo//?imgmax=800)
![clip_image030[1] clip_image030[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEisa4IrHgphMIKj7yrz4-wwgR-VMCUD0ZONhg17UDOOnEowLnmSy6UwwEmDJmQTgvihxRjakXyzHLK19bvFjGyFJG-wVjIsD_HWqtyy_l9wtlLfBQAr8pObaqxHkYmvEr6DanRq-ar3gZQ//?imgmax=800)
![clip_image032[1] clip_image032[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiZQmbQjyLhK4UBxdTpBpE0rtmJDpG4FCLM-R__lbcUMoU5Rwr9Q6B9CWoPc6ktUOY3D0RJxXdTs6-h5QzdI8uBfL5gVEwZgZn3Ekdo5UeDE-l8R3-NOiLA_Skp9qpTBk9IdxKYHhx7yxM//?imgmax=800)
No comments:
Post a Comment