Business Statistics: For Contemporary Decision Making, 8th Edition solutions manual and test bank

Business Statistics: For Contemporary Decision Making, 8th Edition solutions manual and test bank

 

Business Statistics: For Contemporary Decision Making, 8th Edition solutions manual and test bank Ken Black

 

This text is an unbound, binder-ready edition.

Business Statistics: For Contemporary Decision Making, 8th Edition continues the tradition of presenting and explaining the wonders of business statistics through the use of clear, complete, student-friendly pedagogy. Ken Black's text equips readers with the quantitative decision-making skills and analysis techniques you need to make smart decisions based on real-world data.

Table of Contents

UNIT I INTRODUCTION

1 Introduction to Statistics 02

2 Charts and Graphs 18

3 Descriptive Statistics 52

4 Probability 98

UNIT II DISTRIBUTIONS AND SAMPLING

5 Discrete Distributions 142

6 Continuous Distributions 184

7 Sampling and Sampling Distributions 224

UNIT III MAKING INFERENCES ABOUT POPULATION PARAMETERS

8 Statistical Inference: Estimation for Single Populations 260

9 Statistical Inference: Hypothesis Testing for Single Populations 298

10 Statistical Inferences About Two Populations 354

11 Analysis of Variance and Design of Experiments 414

UNIT IV REGRESSION ANALYSIS AND FORECASTING

12 Simple Regression Analysis and Correlation 476

13 Multiple Regression Analysis 528

14 Building Multiple Regression Models 558

15 Time-Series Forecasting and Index Numbers 608

UNIT V NONPARAMETRIC STATISTICS AND QUALITY

16 Analysis of Categorical Data 664

17 Nonparametric Statistics 688

18 Statistical Quality Control 738

APPENDICES

A Tables 783

B Answers to Selected Odd-Numbered Quantitative Problems 823

GLOSSARY 833

INDEX 843

Chapter 2

Charts and Graphs

LEARNING OBJECTIVES

The overall objective of Chapter 2 is for you to master several techniques

for summarizing and depicting data, thereby enabling you to:

1. Construct a frequency distribution from a set of data

2. Construct different types of quantitative data graphs, including

histograms, frequency polygons, ogives, dot plots, and stem-and-leaf

plots, in order to interpret the data being graphed

3. Construct different types of qualitative data graphs, including pie charts,

bar graphs, and Pareto charts, in order to interpret the data being

graphed

4. Construct a cross-tabulation table and recognize basic trends in two-variable

scatter plots of numerical data.

CHAPTER TEACHING STRATEGY

Chapter 1 brought to the attention of students the wide variety and amount of data available in the world of business. In chapter 2, we confront the problem of trying to begin to summarize and present the data in a meaningful manner. One mechanism for data summarization is the frequency distribution which is essentially a way of organizing ungrouped or raw data into grouped data. It is important to realize that there is considerable art involved in constructing a frequency distribution. There are nearly as many possible frequency distributions for a problem as there are students in a class. Students should begin to think about the receiver or user of their statistical product. For example, what class widths and class endpoints would be most familiar and meaningful to the end user of the distribution? How can the data best be communicated and summarized using the frequency distribution?

The second part of chapter 2 presents various ways to depict data using graphs. The student should view these graphical techniques as tools for use in communicating characteristics of the data in an effective manner. Most business students will have some type of management opportunity in their field before their career ends. The ability to make effective presentations and communicate their ideas in succinct, clear ways is an asset. Through the use of graphics packages and such techniques as frequency polygons, ogives, histograms, and pie charts, the manager can enhance his/her personal image as a communicator and decision-maker. In addition, emphasize that the final product (the frequency polygon, etc.) is just the beginning. Students should be encouraged to study the graphical output to recognize business trends, highs, lows, etc. and realize that the ultimate goal for these tools is their usage in decision making.

CHAPTER OUTLINE

2.1 Frequency Distributions

Class Midpoint

Relative Frequency

Cumulative Frequency

2.2 Quantitative Data Graphs

Histograms

Using Histograms to Get an Initial Overview of the Data

Frequency Polygons

Ogives

Dot Plots

Stem and Leaf Plots

2.3 Qualitative Data Graphs

Pie Charts

Bar Graphs

Pareto Charts

2.4 Charts and Graphs for Two Variables

Cross Tabulation

Scatter Plot

KEY TERMS

Bar Graph Histogram

Class Mark Ogive

Class Midpoint Pareto Chart

Cross Tabulation Pie Chart

Cumulative Frequency Range

Dot Plot Relative Frequency

Frequency Distribution Scatter Plot

Frequency Polygon Stem-and-Leaf Plot

Grouped Data Ungrouped Data

SOLUTIONS TO PROBLEMS IN CHAPTER 2

2.1

a) One possible 5 class frequency distribution:

Class Interval Frequency

0 - under 20 7

20 - under 40 15

40 - under 60 12

60 - under 80 12

80 - under 100 4

50

b) One possible 10 class frequency distribution:

Class Interval Frequency

10 - under 18 7

18 - under 26 3

26 - under 34 5

34 - under 42 9

42 - under 50 7

50 - under 58 3

58 - under 66 6

66 - under 74 4

74 - under 82 4

82 - under 90 2

c) The ten class frequency distribution gives a more detailed breakdown of temperatures, pointing out the smaller frequencies for the higher temperature intervals. The five class distribution collapses the intervals into broader classes making it appear that there are nearly equal frequencies in each class.

2.2 a) One possible frequency distribution is the one below with 12 classes and class

intervals of 2.

Class Interval Frequency

39 - under 41 2

41 - under 43 1

43 - under 45 5

45 - under 47 10

47 - under 49 18

49 - under 51 13

51 - under 53 15

53 - under 55 15

55 - under 57 7

57 - under 59 9

59 - under 61 4

61 – under 63 1

b) The distribution reveals that only 13 of the 100 boxes of raisins contain 50 ± 1

raisin (49 -under 51). However, 71 of the 100 boxes of raisins contain between 45 and 55 raisins. It shows that there are five boxes that have 9 or more extra raisins (59-61 and 61-63) and two boxes that have 9-11 less raisins (39-41) than the boxes are supposed to contain.

2.3

Class Class Relative Cumulative

Interval Frequency Midpoint Frequency Frequency

0 - 5 6 2.5 6/86 = .0698 6

5 - 10 8 7.5 .0930 14

10 - 15 17 12.5 .1977 31

15 - 20 23 17.5 .2674 54

20 - 25 18 22.5 .2093 72

25 - 30 10 27.5 .1163 82

30 - 35 4 32.5 .0465 86

TOTAL 86 1.0000

The relative frequency tells us that it is most probable that a customer is in the

15 - 20 category (.2674). Over two thirds (.6744) of the customers are between 10

and 25 years of age.

2.4

Class Class Relative Cumulative

Interval Frequency Midpoint Frequency Frequency

0-2 218 1 .436 218

2-4 207 3 .414 425

4-6 56 5 .112 481

6-8 11 7 .022 492

8-10 8 9 .016 500

TOTAL 500 1.000

2.5 Some examples of cumulative frequencies in business:

sales for the fiscal year,

costs for the fiscal year,

spending for the fiscal year,

inventory build-up,

accumulation of workers during a hiring buildup,

production output over a time period.

2.6 Histogram:

Frequency Polygon:

Comment: The assembly times “pile up” near the middle of the graphs indicating

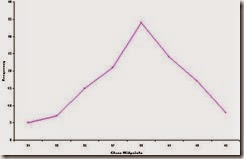
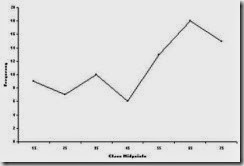
that many of the assembly times are between 36 and 42 minutes.

2.7 Histogram:

Frequency Polygon:

Comment: The histogram indicates that the number of calls per shift varies widely.

However, the heavy numbers of calls per shift fall in the 50 to 80 range.

Since these numbers occur quite frequently, staffing planning should be done

with these number of calls in mind realizing from the rest of the graph that

there may be shifts with as few as 10 to 20 calls.

2.8 Ogive:

2.9 STEM LEAF

21 2 8 8 9

22 0 1 2 4 6 6 7 9 9

23 0 0 4 5 8 8 9 9 9 9

24 0 0 3 6 9 9 9

25 0 3 4 5 5 7 7 8 9

26 0 1 1 2 3 3 5 6

27 0 1 3

Dotplot

Both the stem and leaf plot and the dot plot indicate that sales prices vary quite a bit

within the range of $212,000 and $273,000. It is more evident from the stem and leaf plot that there is a strong grouping of prices in the five price ranges from the $220’s through the $260’s.

2.10 a)

b) STEM LEAF

1 3 6 7 7 7 9 9 9

2 0 3 3 5 7 8 9 9

3 2 3 4 5 7 8 8

4 1 4 5 6 6 7 7 8 8 9

5 0 1 2 2 7 8 9

6 0 1 4 5 6 7 9

7 0 7

8 0

The stem and leaf plot shows that the number of passengers per flight were

relatively evenly distributed between the high teens through the sixties. Rarely

was there a flight with at least 70 passengers. The category of 40's contained the

most flights (10).

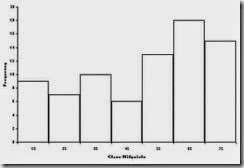
2.11 The histogram shows that there are only three airports with more than 70 million passengers. From the information given in the problem, we know that the busiest airport is Atlanta’s Hartsfield-Jackson International Airport which has over 95 million passengers. We can tell from the graph that there is one airport with between 80 and 90 million passengers and another airport with between 70 and 80 million passengers. Four airports have between 60 and 70 million passengers. Eighteen of the top 30 airports have between 40 and 60 million passengers.

2.12 The dotplot shows that all but one state has 105,000 farms or less. There is only one state with more than 105,000 farms and that state has around 220,000 farms. Most of the states have between a few hundred and about 95,000 farms. There are 7 states that appear to have around 5,000 farms (modal number). Four states have about 10,000 farms, four states have about 30,000 farms, four states have about 45,000 farms, and four states have about 75,000 farms. If one were to ignore the two highest states as outliers, the average of the others would appear to be around 40,000 which is close to the actual mean. While the two largest states tend to increase the mean, the two states are only 4% of the total and therefore only have a moderate effect on the mean.

2.13 From the stem and leaf display, the original raw data can be obtained. For example, the fewest number of cars washed on any given day are 25, 29, 29, 33, etc. The most cars washed on any given day are 141, 144, 145, and 147. The modal stems are 3, 4, and 10 in which there are 6 days with each of these numbers. Studying the left column of the Minitab output, it is evident that the median number of cars washed is 81. There are only two days in which 90 some cars are washed (90 and 95) and only two days in which 130 some cars are washed (133 and 137).

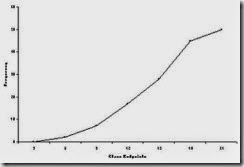
2.14 The ogive tells us several things. Out of 200 pots, 50 of them contained only 10 King crabs. From the ogive, it is possible to see that nearly 100 (or about ½) have 30 or fewer crabs. Almost ¾ of the pots have fewer than 60 crabs. A quick observation of the graph shows that only a very small number (less than 10%) have as many as 100 crabs.

2.15 Firm Proportion Degrees

Intel Corp. .5624 202.5

Texas Instruments .1594 57.4

Qualcomm .1141 41.1

Micron Technology .0831 29.9

Broadcom .0810 29.2

TOTAL 1.0000 360.1

a.) Bar Graph:

File: ch02, Chapter 2: Charts and Graphs

True/False

1. A summary of data in which raw data are grouped into different intervals and the number of items in each group is listed is called a frequency distribution.

Ans: True

Response: See section 2.1 Frequency Distributions

Difficulty: Easy

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

2. If the individual class frequency is divided by the total frequency, the result is the median frequency.

Ans: False

Response: See section 2.1 Frequency Distributions

Difficulty: Medium

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

3. A cumulative frequency distribution provides a running total of the frequencies in the classes.

Ans: True

Response: See section 2.1 Frequency Distributions

Difficulty: Medium

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

4. The difference between the highest number and the lowest number in a set of data is called the differential frequency.

Ans: False

Response: See section 2.1 Frequency Distributions

Difficulty: Medium

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

5. For any given data set, a frequency distribution with a larger number of classes will always be better than the one with a smaller number of classes.

Ans: False

Response: See section 2.1 Frequency Distributions

Difficulty: Medium

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

6. One rule that must always be followed in constructing frequency distributions is that the adjacent classes must overlap.

Ans: False

Response: See section 2.1 Frequency Distributions

Difficulty: Medium

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

7. An instructor made a frequency table of the scores his students got on a test

Score Frequency

30-under 40 1

40-under 50 4

50-under 60 5

60-under 70 10

70-under 80 20

80-under 90 10

90-under 100 5

The midpoint of the last class interval is _________.

a) 90

b) 5

c) 95

d) 100

e) 50

Ans: c

Response: See section 2.1 Frequency Distributions

Difficulty: Easy

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

8. An instructor made a frequency table of the scores his students got on a test

Score Frequency

30-under 40 1

40-under 50 4

50-under 60 5

60-under 70 10

70-under 80 20

80-under 90 10

90-under 100 5

Approximately what percent of students got more than 70?

a) 36

b) 20

c) 50

d) 10

e) 64

Ans: e

Response: See section 2.1 Frequency Distributions

Difficulty: Easy

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

9. A cumulative frequency polygon is also called an ogive.

Ans: True

Response: See section 2.2 Quantitative Data Graphs

Difficulty: Medium

Learning Objective: 2.2: Construct different types of quantitative data graphs, including histograms, frequency polygons, ogives, dot plots, and stem-and-leaf plots, in order to interpret the data being graphed.

10. A histogram can be described as a type of vertical bar chart.

Ans: True

Response: See section 2.2 Quantitative Data Graphs

Difficulty: Medium

Learning Objective: 2.2: Construct different types of quantitative data graphs, including histograms, frequency polygons, ogives, dot plots, and stem-and-leaf plots, in order to interpret the data being graphed.

11. One advantage of a stem and leaf plot over a frequency distribution is that the values of the original data are retained.

Ans: True

Response: See section 2.2 Quantitative Data Graphs

Difficulty: Medium

Learning Objective: 2.2: Construct different types of quantitative data graphs, including histograms, frequency polygons, ogives, dot plots, and stem-and-leaf plots, in order to interpret the data being graphed.

12. For a company in gardening supplies business, the best graphical way to show the percentage of a total budget that is spent on each of a number of different expense categories is the stem and leaf plot.

Ans: False

Response: See section 2.2 Quantitative Data Graphs

Difficulty: Hard

Learning Objective: 2.2: Construct different types of quantitative data graphs, including histograms, frequency polygons, ogives, dot plots, and stem-and-leaf plots, in order to interpret the data being graphed.

13. In a histogram, the tallest bar represents the class with the highest cumulative frequency.

Ans: False

Response: See section 2.2 Quantitative Data Graphs

Difficulty: Medium

Learning Objective: 2.2: Construct different types of quantitative data graphs, including histograms, frequency polygons, ogives, dot plots, and stem-and-leaf plots, in order to interpret the data being graphed.

14. Dot Plots are mainly used to display a large data set.

Ans: False

Response: See section 2.2 Quantitative Data Graphs

Difficulty: Medium

Learning Objective: 2.2: Construct different types of quantitative data graphs, including histograms, frequency polygons, ogives, dot plots, and stem-and-leaf plots, in order to interpret the data being graphed.

15. A graphical representation of a frequency distribution is called a pie chart.

Ans: False

Response: See section 2.3 Qualitative Data Graphs

Difficulty: Easy

Learning Objective: 2.3: Construct different types of qualitative data graphs, including pie charts, bar graphs, and Pareto charts, in order to interpret the data being graphed.

16. In contrast to quantitative data graphs that are plotted along a numerical scale, qualitative graphs are plotted using non-numerical categories.

Ans: True

Response: See section 2.3 Qualitative Data Graphs

Difficulty: Easy

Learning Objective: 2.3: Construct different types of qualitative data graphs, including pie charts, bar graphs, and Pareto charts, in order to interpret the data being graphed.

17. A Pareto chart and a pie chart are both types of qualitative graphs.

Ans: True

Response: See section 2.3 Qualitative Data Graphs

Difficulty: Easy

Learning Objective: 2.3: Construct different types of qualitative data graphs, including pie charts, bar graphs, and Pareto charts, in order to interpret the data being graphed.

18. A scatter plot shows how the numbers in a data set are scattered around their average.

Ans: False

Response: See section 2.4 Charts and Graphs for Two Variables.

Difficulty: Medium

Learning objective: 2.4: Recognize basic trends in two-variable scatter plots of numerical data.

19. A scatter plot is a two-dimensional graph plot of data containing pairs of observations on two numerical variables.

Ans: True

Response: See section 2.4 Charts and Graphs for Two Variables

Difficulty: Medium

Learning objective: 2.4: Recognize basic trends in two-variable scatter plots of numerical data.

20. A scatter plot is useful for examining the relationship between two numerical variables.

Ans: True

Response: See section 2.4 Charts and Graphs for Two Variables

Difficulty: Medium

Learning objective: 2.4: Recognize basic trends in two-variable scatter plots of numerical data.

Multiple Choice

21. Consider the following frequency distribution:

Class Interval Frequency

10-under 20 15

20-under 30 25

30-under 40 10

What is the midpoint of the first class?

a) 10

b) 20

c) 15

d) 30

e) 40

Ans: c

Response: See section 2.1 Frequency Distributions

Difficulty: Easy

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

22. Consider the following frequency distribution:

Class Interval Frequency

10-under 20 15

20-under 30 25

30-under 40 10

What is the relative frequency of the first class?

a) 0.15

b) 0.30

c) 0.10

d) 0.20

e) 0.40

Ans: b

Response: See section 2.1 Frequency Distributions

Difficulty: Medium

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

23. Consider the following frequency distribution:

Class Interval Frequency

10-under 20 15

20-under 30 25

30-under 40 10

What is the cumulative frequency of the second class interval?

a) 25

b) 40

c) 15

d) 50

Ans: b

Response: See section 2.1 Frequency Distributions

Difficulty: Medium

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

24. The number of phone calls arriving at a switchboard each hour has been recorded, and the following frequency distribution has been developed.

Class Interval Frequency

20-under 40 30

40-under 60 45

60-under 80 80

80-under 100 45

What is the midpoint of the last class?

a) 80

b) 100

c) 95

d) 90

e) 85

Ans: d

Response: See section 2.1 Frequency Distributions

Difficulty: Easy

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

25. The number of phone calls arriving at a switchboard each hour has been recorded, and the following frequency distribution has been developed.

Class Interval Frequency

20-under 40 30

40-under 60 45

60-under 80 80

80-under 100 45

What is the relative frequency of the second class?

a) 0.455

b) 0.900

c) 0.225

d) 0.750

e) 0.725

Ans: c

Response: See section 2.1 Frequency Distributions

Difficulty: Medium

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

26. The number of phone calls arriving at a switchboard each hour has been recorded, and the following frequency distribution has been developed.

Class Interval Frequency

20-under 40 30

40-under 60 45

60-under 80 80

80-under 100 45

What is the cumulative frequency of the third class?

a) 80

b) 0.40

c) 155

d) 75

e) 105

Ans: c

Response: See section 2.1 Frequency Distributions

Difficulty: Medium

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

27 A person has decided to construct a frequency distribution for a set of data containing 60 numbers. The lowest number is 23 and the highest number is 68. If 5 classes are used, the class width should be approximately _______.

a) 4

b) 12

c) 8

d) 5

e) 9

Ans: e

Response: See section 2.1 Frequency Distributions

Difficulty: Easy

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

28. A person has decided to construct a frequency distribution for a set of data containing 60 numbers. The lowest number is 23 and the highest number is 68. If 7 classes are used, the class width should be approximately _______.

a) 5

b) 7

c) 9

d) 11

e) 12

Ans: b

Response: See section 2.1 Frequency Distributions

Difficulty: Medium

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

29. A frequency distribution was developed. The lower endpoint of the first class is 9.30, and the midpoint is 9.35. What is the upper endpoint of this class?

a) 9.50

b) 9.60

c) 9.70

d) 9.40

e) 9.80

Ans: d

Response: See section 2.1 Frequency Distributions

Difficulty: Medium

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

30. The cumulative frequency for a class is 27. The cumulative frequency for the next (non-empty) class will be _______.

a) less than 27

b) equal to 27

c) next class frequency minus 27

d) 27 minus the next class frequency

e) 27 plus the next class frequency

Ans: e

Response: See section 2.1 Frequency Distributions

Difficulty: Hard

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

31. The following class intervals for a frequency distribution were developed to provide information regarding the starting salaries for students graduating from a particular school:

Salary Number of Graduates

($1,000s)

28-under 31 -

31-under 35 -

34-under 37 -

39-under 40 -

Before data was collected, someone questioned the validity of this arrangement. Which of the following represents a problem with this set of intervals?

a) There are too many intervals.

b) The class widths are too small.

c) Some numbers between 28,000 and 40,000 would fall into two different intervals.

d) The first and the second interval overlap.

e) There are too few intervals.

Ans: c

Response: See section 2.1 Frequency Distributions

Difficulty: Medium

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

32. The following class intervals for a frequency distribution were developed to provide information regarding the starting salaries for students graduating from a particular school:

Salary Number of Graduates

($1,000s)

28-under 31 -

31-under 35 -

34-under 37 -

39-under 40 -

Before data was collected, someone questioned the validity of this arrangement. Which of the following represents a problem with this set of intervals?

a) There are too many intervals.

b) The class widths are too small.

c) Some numbers between 28,000 and 40,000 would not fall into any of these intervals.

d) The first and the second interval overlap.

e) There are too few intervals.

Ans: c

Response: See section 2.1 Frequency Distributions

Difficulty: Hard

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

33. The following class intervals for a frequency distribution were developed to provide information regarding the starting salaries for students graduating from a particular school:

Salary Number of Graduates

($1,000s)

28-under 31 -

31-under 35 -

34-under 37 -

39-under 340 -

Before data was collected, someone questioned the validity of this arrangement. Which of the following represents a problem with this set of intervals?

a) There are too many intervals.

b) The class widths are too small.

c) The class widths are too large.

d) The second and the third interval overlap.

e) There are too few intervals.

Ans: d

Response: See section 2.1 Frequency Distributions

Difficulty: Medium

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

34. Abel Alonzo, Director of Human Resources, is exploring employee absenteeism at the Harrison Haulers Plant during the last operating year. A review of all personnel records indicated that absences ranged from zero to twenty-nine days per employee. The following class intervals were proposed for a frequency distribution of absences.

Absences Number of Employees

(Days)

0-under 5 -

5-under 10 -

10-under 15 -

20-under 25 -

25-under 30 -

Which of the following represents a problem with this set of intervals?

a) There are too few intervals.

b) Some numbers between 0 and 29, inclusively, would not fall into any interval.

c) The first and second interval overlaps.

d) There are too many intervals.

e) The second and the third interval overlap.

Ans: b

Response: See section 2.1 Frequency Distributions

Difficulty: Medium

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

35. Abel Alonzo, Director of Human Resources, is exploring employee absenteeism at the Harrison Haulers Plant during the last operating year. A review of all personnel records indicated that absences ranged from zero to twenty-nine days per employee. The following class intervals were proposed for a frequency distribution of absences.

Absences Number of Employees

(Days)

0-under 10 -

10-under 20 -

20-under 30 -

Which of the following might represent a problem with this set of intervals?

a) There are too few intervals.

b) Some numbers between 0 and 29 would not fall into any interval.

c) The first and second interval overlaps.

d) There are too many intervals.

e) The second and the third interval overlap.

Ans: a

Response: See section 2.1 Frequency Distributions

Difficulty: Medium

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

36. Consider the relative frequency distribution given below:

Class Interval Relative Frequency

20-under 40 0.2

40-under 60 0.3

60-under 80 0.4

80-under 100 0.1

There were 60 numbers in the data set. How many numbers were in the interval 20-under 40?

a) 12

b) 20

c) 40

d) 10

e) 15

Ans: a

Response: See section 2.1 Frequency Distributions

Difficulty: Easy

Learning Objective: 2.1: Construct a frequency distribution from a set of data.

37. Consider the relative frequency distribution given below:

Class Interval Relative Frequency

20-under 40 0.2

40-under 60 0.3

60-under 80 0.4

80-under 100 0.1

There were 60 numbers in the data set. How many numbers were in the interval 40-under 60?

a) 30

b) 50

c) 18

d) 12

e) 15

Ans: c

Response: See section 2.1 Frequency Distributions

Difficulty: Easy

Learning Objective: 2.1: Construct a frequency distribution from a set of data.