Understanding Statistics in the Behavioral Sciences, 10th Edition Robert R. Pagano solutions manual and test bank
CHAPTER 13
Student’s t Test for Single Samples
LEARNING OBJECTIVES
After completing Chapter 13, students should be able to:
1. Contrast the t test and the z test for single samples.
2. Define degrees of freedom.
3. Define the sampling distribution of t and state its characteristics
4. Compare the t and z distributions.
5. Solve problems using the t test for single samples, and specify the conditions under which the t test for single samples is appropriate.
6. Measure size of effect, using Cohen’s d.
7. Contrast point and interval estimation.
8. Define confidence interval and confidence limits;
9. Define and construct the 95% and 99% confidence limits for the population mean.
10. Determine for the significance of Pearson r, using two methods.
11. Understand the illustrative examples, do the practice problems and understand the solutions.
DETAILED CHAPTER SUMMARY
I. Introduction
A. Use of the t test. Use the t test when
1. the mean of the Null Hypothesis Population can be specified
2. the standard deviation is unknown (which also means the z test cannot be used)
B. Applications covered in this chapter.
1. Analysis of data in experiments with a single sample
2. Determining the significance of Pearson r.
II. Comparison of z and t Tests
A. Formula.
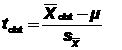
= estimated standard error of the mean =
B. z and t equation differences. Difference between equations is that in the t equation, s and are used instead of and
respectively.
III. Sampling Distribution of t
A. Definition. the sampling distribution of t is a probability distribution of the t values which would occur if all possible different samples of a fixed size N were drawn from the Null Hypothesis Population. It gives (1) all the possible t values for samples of size N and (2) the probability of getting each value if sampling is random from the Null Hypothesis Population.
B. Characteristics.
1. Family of curves; many curves with a different curve for each sample size N.
2. Shape. Shaped similarly to z distribution if
a. sample size ³ 30 or
b. H0 population is normally distributed.
C. Degrees of freedom (df). The number of scores that are free to vary.
df = N -1
D. Comparison of z and t distributions.
1. t and z are both symmetrical about 0
2. As df increases t becomes more similar to z
3. As df approaches ¥, t becomes identical to z
4. At any value of df < ¥, the t distribution has more extreme values than z (i.e., tails of the t distribution are more elevated than in the z distribution)
5. For a given alpha level, tcrit > zcrit
IV. Calculations and Use of t
A. Calculation of t from raw scores.
B. Requirements. Appropriate use of t requires that sampling distribution of is normal. This can result if N ³ 30 or population of raw scores is normal.
V. Size of Effect Using Cohen’s d
A. Rationale. The statistic we are using to measure size of effect is symbolized by “d.” It is a standardized statistic that relies on the relationship between the size of effect and . As the size of effect gets greater, so does
, regardless of the direction of the effect. The statistic d uses the absolute value of
since we are interested in the size of real effect, and are not concerned about direction. This allows d to have a positive value that increases with the size of the difference between
and μ regardless of the direction of the real effect.
is divided by σ to create a standardized value, much as was done with z scores.
B. Formula for Cohen’s d.
Conceptual equation for size of effect, single sample t test
Since σ is unknown, we estimate it using s, the sample standard deviation. Substituting s for σ, we arrive at the computational equation for size of effect. Since s is an estimate, is used instead of d.
Computational equation for size of effect, single sample t test
C. Interpreting the Value of . To interpret the value of
, we are using the criteria that Cohen has provided. These criteria are given in the following table.
| 0.00 – 0.20 | Small effect |
| 0.21 – 0.79 | Medium effect |
| ≥0.80 | Large effect |
VI. Confidence Intervals for the Population Mean
A. Definition. A confidence interval is a range of values which probably contains the population mean. Confidence limits are the values that bound the confidence interval. Example: The 95% confidence interval is an interval such that the probability is 0.95 that the interval contains the population value.
B. Formula for confidence interval.
VII. Testing Significance of Pearson r.
A. Rho (). this is the Greek letter to symbolize the population correlation coefficient.
B. Nondirectional H0. Asserts ¹ 0.
C. Directional H0 Asserts that is positive or negative depending on the predicted direction of the relationship.
D. Sampling distribution of r. Generated by taking all samples of size N from a population in which = 0 and calculating r for each sample. By systematically varying the population scores and N, the sampling distribution of r is generated.
E. Using t test to evaluate significance of r:
with df = N - 2 and N equals the number of pairs of X, Y scores.
F. Using rcrit to evaluate the significance of r:
if | robt | ³ | rcrit |, reject H0
The values of rcrit can be calculated directly. Values of rcrit are shown in Table E.
TEACHING SUGGESTIONS AND COMMENTS
In many ways this chapter is a continuation of the z test for single samples, only now we are dealing with situations in which σ is unknown and therefore we must estimate it with s. In addition to discussing hypothesis testing using the t test for single samples, the chapter includes two other uses of the t test, constructing confidence intervals and testing the significance of Pearson r. Again I believe the chapter works well and recommend sticking close to it, using the same examples. I lecture on all topics in this chapter, except Testing the Significance of Pearson r. My students are not required to learn this topic. While this topic is of some importance, with the limited time available, I do not believe it warrants inclusion. Specific comments and suggestions are as follows.
1. Comparison of the z and t tests. The important point to make here is that the t test is very much like the z test except that it is used in situations where σ is unknown. σ is estimated by using s and when s is substituted for σ in the z equation, the equation becomes the t equation. Students grasp this point easily.
2. The sampling distribution of t. The major difference here is that there are a family of sampling distributions of t, instead of just one as is true for z. A subtle point regarding this section, that needs emphasizing is that as N increases, the sampling distribution of t approaches that of the sampling distribution of z, namely the normal distribution. I refer to figure 13.1 on p. 331 when discussing this point. The practical reason this is important is that the sampling distribution of z is lower at the tails then the sampling distribution of t, resulting in greater power using the z test. To see if they appreciate this point, I like giving a computational question on the exam that gives both σ and s and letting them analyze the data with the equation they think is the appropriate one. I often also manipulate the data such that the results are significant using the z equation, but not using the t equation.
3. Early speaking experiment revisited. Analyzing the data with the t test is very similar to doing so with the z test. The one major difference is that determining tcrit involves calculating df and well as knowing α. Students don’t seem to have any difficulties with computing tobt or determining tcrit. Of course if you require them to compute tobt from raw scores, rather than giving them s, they are likely to make more calculation errors.
4. Size of effect using Cohen’s d. I haven’t had enough experience teaching this section to offer recommendations. However, it seems like a relatively easy section to teach and to learn. A somewhat difficult conceptual point is why absolute values are used.
5. Construction of the 95% confidence interval. The derivation of the equations for uupper and ulower, given on p. 341-342, is a little difficult for students. Another hard concept for them to grasp is the statement on p. 343, “Note that the probability value applies to the interval and not to the population mean. The population mean is constant. What varies from sample to sample is the interval. Thus, it is not technically proper to state, the probability is 0.95 that the population mean lies within the interval. Rather, the proper statement is ‘the probability is 0.95 that the interval contains the population mean.” I sometimes test understanding of this point with a short essay question. The question might go something like this. When constructing the 95% confidence interval, it is improper to say that the probability is 0.95 that the interval contains the population mean. Is this statement true? Explain. I regard this question as a difficult one. When constructing the 95% and 99% confidence intervals, one rather common mistake students make is to use s instead of . Otherwise, students are able to construct the 95% and 99% confidence intervals with little difficulty.
6. Testing the significance of Pearson r. Even though I usually don’t cover this section in my introductory course, there are some comments that I would like to offer. The section presents two methods for testing the significance of Pearson r. The second method, in which robt is compared with rcrit, is the preferred method; the first method is necessary to provide the understanding needed for the second method. I recommend only spending time on the first method necessary to provide the basis for moving on to the preferred, second method.
Even if you don’t teach this section, I believe it is worth mentioning to students that the correlation coefficient we’ve referred to as r is a statistic obtained from sample data and that before one can conclude it represents a real relationship in the population, rather than being due to chance, an inference test needs to be conducted. This surprises them. They are so used to reading about correlations reported in the popular press without accompanying significance testing that they have come to believe that the reported sample correlation is real without requiring the necessary significance testing. This is a very good opportunity to correct this error and of course to tell them that the inference test to use is the t test for single samples.
DISCUSSION QUESTIONS
1. Compare the z test and t test for single samples. What are the advantages and disadvantages of each? Discuss.
2. In presenting the t test for single samples, it was necessary to introduce the concept of degrees of freedom. However, no such discussion was needed in presenting the z test for single samples. What is the explanation of this difference? Discuss.
3. The 95% confidence interval is defined as an interval such that the probability is 0.95 that the interval contains the population value. Another possible way of stating this is that the 95% confidence interval is an interval such that that the probability is 0.95 that the population value is contained in the interval. Are these two wordings equivalent, or is one technically more correct than the other? Discuss.
4. Does a significant robt value, calculated on sample data prove that there is a relationship in the population? Discuss.
5. Why do you suppose that the value used to measure the size of real effect is a standardized value? Discuss.
6. Explain why the size of the difference between is used as the basic variable for estimating the size of real effect. Discuss.
TEST QUESTIONS
MULTIPLE CHOICE
1. In an independent groups experiment, if we must estimate the population standard deviation to determine the significance of the sample results, the appropriate inference test is the _________.
| a. | sign test | c. | t test |
| b. | z test | d. | none of these |
ANS: C
2. For a given N, the interval that bounds the population mean at the 99% confidence level is _________ that which bounds the population mean at the 95% confidence level.
| a. | equal to |
| b. | greater than |
| c. | less than |
| d. |
ANS: C
3. The mean of the t distribution equals _________.
| a. | the mean of the population of raw scores |
| b. | 0 |
| c. | 1 |
| d. | |
ANS: B
4. | tcrit | for any alpha level is _________ | zcrit | for N less than infinity.
| a. | greater than | c. | less than |
| b. | the same as | d. | none of these |
ANS: A
5. Which of the following represents a sampling distribution?
| a. | the binomial distribution |
| b. | the z distribution |
| c. | the t distribution |
| d. | all of these |
| e. | the z and t distributions |
ANS: D
6. When using the t test, we reject H0 _________.
| a. | if tobt tcrit | c. | if | tobt | | tcrit | |
| b. | if | tobt | | tcrit | | d. | if tobt tcrit |
ANS: B
7. The sampling distribution of t depends on _________.
| a. | µ |
| b. | |
| c. | s |
| d. | df |
| e. | |
| f. | all of these |
ANS: D
8. In a t test, when the size of the sample is increased, the confidence interval _________.
| a. | increases | c. | stays the same |
| b. | decreases | d. | changes shape |
ANS: B
9. The 95% confidence interval arrived at from a particular experiment is 72-79. This means that _________.
| a. | the probability is 0.95 that µ falls between 72-79 |
| b. | |
| c. | the probability is 0.95 that the interval 72-79 contains µ |
| d. | a and c |
ANS: C
10. Which of the characteristics below distinguishes the t statistic from the z statistic?
| a. | the proportion of area beyond a particular positive t value is equal to the proportion of area below the corresponding negative t |
| b. | the z distribution has a mean of zero while the t distribution does not |
| c. | In the t distribution the area under the curve beyond a value of ±1.96 is greater than that of the normal curve |
| d. | all of these |
ANS: C
11. As the df increases, the t distribution _________.
| a. | gets more symmetrical | c. | stays the same |
| b. | approaches the normal distribution | d. | becomes more skewed |
ANS: B
12. With which statistical test do we determine the probability of getting the obtained results or those more extreme assuming the differences in results were due to chance alone?
| a. | sign test | c. | t test |
| b. | z test | d. | all of these |
ANS: D
13. In a correlated groups experiment, if we must estimate the population standard deviation to determine the significance of the sample results, the appropriate statistical test is _________.
| a. | t test | c. | z test |
| b. | sign test | d. | none of these |
ANS: A
14. As the degrees of freedom increase, the correspondence between the t and z distributions _________.
| a. | increases | c. | remains the same |
| b. | decreases | d. | cannot be determined |
ANS: A
15. The t test differs from the z test in that _________.
| a. | with the t test we estimate |
| b. | with the t test we estimate µ |
| c. | the z distribution is a family of curves |
| d. | the t distribution is a family of curves |
| e. | with the t test we estimate and the t distribution is a family of curves |
ANS: E
16. is an estimate of _________.
| a. | µ | c. | |
| b. | | d. | s |
ANS: C
17. We lose one degree of freedom in calculating _________.
| a. | s | c. | tobt (single sample) |
| b. | d. | s and tobt (single sample) |
ANS: D
18. The degrees of freedom for the t test for single samples are _________.
| a. | N | c. | N 2 |
| b. | N 1 | d. | depends on alpha |
ANS: B
19. The confidence interval for the population mean is _________.
| a. | a range of values which probably contains the population mean |
| b. | a range of values which contains the population mean |
| c. | the same from sample-to-sample |
| d. | a range of values which probably contains the population mean and the same from sample-to-sample |
ANS: A
20. In a correlative study, _________.
| a. | a value of r 0 in the sample, means that there is a nonzero correlation in the population |
| b. | a nondirectional alternative hypothesis states that 0 |
| c. | the null hypothesis for a nondirectional alternative hypothesis states that = 0 |
| d. | a nondirectional alternative hypothesis states that r = 0 |
| e. | a nondirectional alternative hypothesis states that 0 and the null hypothesis for a nondirectional alternative hypothesis states that = 0 |
ANS: E
21. The df associated with evaluating the significance of robt are _________.
| a. | N | c. | N 2 |
| b. | N 1 | d. | need more information |
ANS: C
22. A researcher believes that women today weigh less than in previous years. To investigate this belief, she randomly samples 41 adult women and records their weights. The scores have a mean of 111 lbs. and a standard deviation of 12.4. A local census taken several years ago shows the mean weight of adult women was 115 lbs.
The obtained value of the appropriate statistic for testing H0 is _________.
| a. | tobt = 2.07 | c. | tobt = 0.32 |
| b. | tobt = +2.07 | d. | tobt = +0.32 |
ANS: A
23. A researcher believes that women today weigh less than in previous years. To investigate this belief, she randomly samples 41 adult women and records their weights. The scores have a mean of 111 lbs. and a standard deviation of 12.4. A local census taken several years ago shows the mean weight of adult women was 115 lbs.
The df for determining tcrit = _________.
| a. | 41 | c. | 39 |
| b. | 40 | d. | need more information |
ANS: B
24. A researcher believes that women today weigh less than in previous years. To investigate this belief, she randomly samples 41 adult women and records their weights. The scores have a mean of 111 lbs. and a standard deviation of 12.4. A local census taken several years ago shows the mean weight of adult women was 115 lbs.
Using = 0.011 tail, the critical value of the appropriate statistic for testing H0 is _________.
| a. | 1.684 | c. | ±1.684 |
| b. | 2.423 | d. | ±2.423 |
ANS: B
25. A researcher believes that women today weigh less than in previous years. To investigate this belief, she randomly samples 41 adult women and records their weights. The scores have a mean of 111 lbs. and a standard deviation of 12.4. A local census taken several years ago shows the mean weight of adult women was 115 lbs.
What do you conclude, using the appropriate inference test and = 0.011 tail?
| a. | accept H1 |
| b. | accept H0 |
| c. | reject H0 |
| d. | retain H0 |
| e. | accept H1 and reject H0 |
ANS: D
26. Use the data presented in the text, Chapter 7, question 12. In that question, robt = 0.69 and N = 10. Using = 0.052 tail, is this a significant value for robt?
| a. | Yes, df = 9, rcrit = ±0.6021 | c. | Yes, df = 8, rcrit = 0.6319 |
| b. | Yes, df = 8, rcrit = ±0.6319 | d. | Yes, df = 8, rcrit = +0.6319 |
ANS: B
27. The 95% confidence interval of the mean for = 13.0, s = 1.6, and N = 21 is _________.
| a. | 12.01 to 13.99 | c. | 11.05 to 15.05 |
| b. | 12.27 to 13.73 | d. | 12.95 to 14.95 |
ANS: B MSC: WWW
28. How many t distributions are there?
| a. | 1 | c. | 30 |
| b. | 2 | d. | one for each value of df |
ANS: D MSC: WWW
29. The mean of the t distribution equals _________.
| a. | 0 | c. | N |
| b. | 1 | d. | N 1 |
ANS: A
30. For a given value of alpha, the critical value of t is _______ than the critical value of z.
| a. | no different | c. | greater |
| b. | less | d. | none of these |
ANS: C MSC: WWW
31. As N gets _______, the critical value of t gets _________.
| a. | larger; larger | c. | larger; smaller |
| b. | smaller; smaller | d. | smaller; larger |
ANS: C MSC: WWW
32. As N gets infinitely large, the critical value of t equals the critical value of z.
| a. | true | b. | false |
ANS: A
33. If µ = 30, = 5.2, = 28.0, s = 6.1 and N = 13, the value of the most powerful statistic to test the significance of the sample mean is _________.
| a. | 1.18 | c. | 2.18 |
| b. | 1.96 | d. | 1.39 |
ANS: D MSC: WWW
34. If the population parameters are known, the t test is _________ powerful than the z test.
| a. | more | c. | equally |
| b. | less | d. | need more information |
ANS: B
35. As N increases becomes a _________ estimate of
.
| a. | better | c. | meaningless |
| b. | worse | d. | biased |
ANS: A
36. The proper use of the t test requires that _________.
| a. | |
| b. | N 30 |
| c. | |
| d. |
ANS: D MSC: WWW
37. The _______ confidence interval for the population mean is always wider than the _______ confidence interval for the population mean.
| a. | 99%; 95% | c. | both of these |
| b. | 95%; 99% | d. | none of these |
ANS: A MSC: WWW
38. The sample mean is an example of _________.
| a. | interval estimation | c. | confidence point |
| b. | point estimation | d. | confidence numbers |
ANS: B
39. For N = 20, the degrees of freedom for the test of the significance of the correlation coefficient (r) is _________.
| a. | 20 | c. | 19 |
| b. | 21 | d. | 18 |
ANS: D MSC: WWW
40. For N = 20, the value of rcrit for = 0.052 tail is _________.
| a. | 0.4329 | c. | 0.4438 |
| b. | 0.3783 | d. | 0.5614 |
ANS: C
41. If r = 0.84 and N = 5, the value of tobt for the test of the significance of r is _________.
| a. | 1.96 | c. | 2.68 |
| b. | 2.40 | d. | 3.46 |
ANS: C MSC: WWW
42. Which of the following are not characteristics of the t distribution?
| a. | has a mean = 0. |
| b. | has a standard deviation greater than 1.00 for df less than infinity. |
| c. | varies with df. |
| d. | has no negative values. |
| e. | all of these are characteristics of the t distribution. |
ANS: D MSC: WWW
43. Confidence interval is defined as _________.
| a. | a range of values that probably contains the population value |
| b. | a range of values that probably contains the population mean |
| c. | a range of values that probably contain the population standard deviation |
| d. | all of these |
ANS: A
44. Confidence limits are defined as _________.
| a. | the highest and lowest score in the sample set of scores |
| b. | the values that lie outside of the confidence interval |
| c. | the values that bound the confidence interval |
| d. | the values that lie within the confidence interval |
ANS: C
45. The 95% confidence interval is defined as _________.
| a. | an interval such that we are 95% confident that the population value lies within the interval |
| b. | an interval such that the probability is 0.95 that the interval contains the population value |
| c. | an interval such that we can reject H0 at α = 0.05 |
| d. | a and b |
ANS: B
46. The 99% confidence interval is defined as _________.
| a. | an interval such that we are 99% confident that the population value lies within the interval |
| b. | an interval such that the probability is 0.99 that the interval contains the population value |
| c. | an interval such that we can reject H0 at α = 0.01 |
| d. | an interval such that we are 99% confident that the population value lies within the interval and an interval such that the probability is 0.99 that the interval contains the population value |
ANS: B
47. ”Degrees of freedom” for any statistic is defined as _________.
| a. | N |
| b. | N 1 |
| c. | the number of scores that are free to vary in calculating the statistic |
| d. | N 1and the number of scores that are free to vary in calculating the statistic |
ANS: C
48. The sampling distribution of t _________.
| a. | gives all possible different t values of size N and the probability of getting each value if sampling is random from the null-hypothesis population |
| b. | is defined as a probability distribution of the t values that would occur if all possible different samples of size N were drawn from the null hypothesis population |
| c. | varies uniquely with N |
| d. | all of these |
| e. | a and b |
ANS: E
49. The sampling distribution of t differs from the sampling distribution of z in that _________.
| a. | there is only one sampling distribution of z (the normal distribution) for all N, while there are many sampling distributions for t, depending on sample size. |
| b. | the sampling distribution of z is more narrow, except when N equals infinity. |
| c. | the means of the two distributions are different |
| d. | all of these |
| e. | a and b |
ANS: E
50. In general, the z test is more powerful than the t test because _________.
| a. | with the z test, the sample mean is closer to the population mean than with the t test |
| b. | with the t test we lose a degree of freedom |
| c. | the standard deviation of the sample raw scores is larger with the t test |
| d. | with the z test, we know σ, whereas with the t test, we must estimate it. |
ANS: D
TRUE/FALSE
1. There are two values for tcrit when H1 is directional.
ANS: F
2. As the degrees of freedom increase, the t distribution becomes more like the z distribution.
ANS: T MSC: WWW
3. The t distribution is a family of curves that vary with the degrees of freedom.
ANS: T
4. If we have to estimate , we should use the z test.
ANS: F
5. The degrees of freedom equal N 1 for the t test for single samples.
ANS: T
6. To test the significance of robt, the df = N 2.
ANS: T
7. The t test is more sensitive than the z test.
ANS: F MSC: WWW
8. tcrit must always be positive.
ANS: F
9. The t test requires that the sampling distribution of t be normally distributed.
ANS: F
10. If N < 30, to use the t test, the population of raw scores should be normally distributed.
ANS: T MSC: WWW
11. Generally speaking, the more confidence we have that the interval contains the population mean, the larger is the interval.
ANS: T MSC: WWW
12. determines the confidence interval for the population mean.
ANS: T
13. In general, if r = 0, then = 0.
ANS: F
14. In general, if r 0, then must not equal 0.
ANS: F MSC: WWW
15. If r > 0.50, then there must be a nonzero correlation in the population.
ANS: F
16. If | robt | > | rcrit |, we reject the assumption that = 0.
ANS: T
17. The t test for single samples is used when the population parameters µ and are unknown.
ANS: F MSC: New
18. In the t test s is used to estimate .
ANS: T MSC: New
19. In general tcrit is greater than zcrit at the same level.
ANS: T MSC: New
20. The t test is more powerful than the z test.
ANS: F MSC: New
21. The t distribution is the same for all sample sizes.
ANS: F MSC: New
22. By definition the degrees of freedom for all statistical tests equals N 1.
ANS: F MSC: New
23. The mean of the t distribution equals 0 for all sample sizes.
ANS: T MSC: New
24. When df = the t distribution is identical to the z distribution.
ANS: T MSC: New
25. The t test can only be applied to a nondirectional alternative hypothesis.
ANS: F MSC: New
26. For a two-tailed test, if | tobt | | tcrit |, reject H0.
ANS: T MSC: New
27. The t test requires that the sampling distribution of is normal.
ANS: F MSC: New
28. The confidence interval is one example of point estimation.
ANS: F MSC: New
29. The 95% confidence interval means that 95% of the time = µ.
ANS: F MSC: New
30. The 99% confidence limit is always wider than the 95% confidence interval.
ANS: T MSC: New
31. If robt is not equal to zero, cannot equal zero.
ANS: F MSC: New
32. For the t test of the significance of the correlation coefficient, the statistic of interest is .
ANS: F MSC: New
33. If r = 0.10 and N = 8, cannot equal +0.10.
ANS: F MSC: New
34. If we conclude that there is a significant correlation in the population we may be making a Type I error.
ANS: T MSC: New
35. For the distribution of to be normally distributed, the distribution of X must be normally distributed.
ANS: F MSC: New
36. The larger the sample size the more likely is close to µ.
ANS: T MSC: New
37. At = 0.05 there is more area in the critical region of rejection for the t distribution than for the z distribution.
ANS: F MSC: New
38. Changing sample size has no effect on power when using the t test.
ANS: F MSC: New
39. If = 1.00, then robt must equal 1.00.
ANS: T MSC: New
40. Other variables held constant, the larger the size of the difference between and μ, the larger the size of effect.
ANS: T MSC: New
41. measures both the size of effect and the direction of the effect.
ANS: F MSC: New
42. gives a value in raw score units for the size of effect.
ANS: F MSC: New
SHORT ANSWER
1. Define Cohen’s d.
ANS: Answer not provided
2. Define the 95% confidence interval.
ANS: Answer not provided MSC: WWW
3. Define confidence limits.
ANS: Answer not provided
4. Define critical value(s) of r.
ANS: Answer not provided
5. Define critical value(s) of t.
ANS: Answer not provided
6. Define degrees of freedom.
ANS: Answer not provided MSC: WWW
7. Define sampling distribution of t.
ANS: Answer not provided
8. A researcher believes that women today weigh less than in previous years. To investigate this belief, she randomly samples 41 adult women and records their weights. The scores have a mean of 111 lbs. and a standard deviation of 12.4. A local census taken several years ago shows the mean weight of adult women was 115 lbs.
a. What is the alternative hypothesis?
b. What is the null hypothesis?
c. What is your conclusion, using α = 0.011 tail?
d. What type error may you be making because of your conclusion in part c? Please show all work.
ANS: Answer not provided
9. One of the undergraduate advisors at a state university wants to estimate the average number of hours freshman business majors at her school spend studying each week. He randomly samples 25 freshman business majors from the freshman business majors attending that semester and measures how many hours each spends studying for a three week period. She then averages the results. The results show a mean of 24 hrs/week and a standard deviation of 4.6 hrs/week.
a. Construct the 95% confidence interval for the mean weekly studying time of all of the freshman business majors that are in attendance that semester.
b. Construct the 99% confidence interval for the mean weekly studying time of all of the freshman business majors that are in attendance that semester.
ANS: Answer not provided
10. Define confidence interval and confidence limits.
ANS: Answer not provided
11. Describe the characteristics of the sampling distribution of t.
ANS: Answer not provided MSC: WWW
12. What are the assumptions underlying the t test for single samples.
ANS: Answer not provided
13. Which test, z or t, has higher power? Explain why?
ANS: Answer not provided
14. A study is conducted, and Pearson r is calculated on the sample data. Assume r = 0.77. Does this mean there is a non-zero correlation in the population? Explain.
ANS: Answer not provided
15. For the same set of data, is the 99% confidence interval always larger than the 95% confidence interval? Explain why or why not?
ANS: Answer not provided
16. Write the number of the symbol shown in Column 1 in the space provided to the left of the term in Column 2 that it represents.
| Column 1 Symbols | Column 2 Terms |
| 1. μ 3. s 4. σ | __standard deviation of a population of raw scores __mean of a population of raw scores __estimated standard error of the mean __standard deviation of a sample of raw scores __standard error of the mean |
ANS: Answer not provided MSC: WWW
17. What are the values for the degrees of freedom for samples of the following sizes (assuming one is calculating a t test for a single sample)?
a. 25
b. 24
c. 2
d. 11
e. 9
ANS: Answer not provided MSC: New
18. A sample has a value of = 46, s = 8, and N = 12.
a. What is the value of tobt to test the hypothesis that this sample could reasonably have been drawn from the Null Hypothesis Population with µ = 50?
b. What is the critical value of t using = 0.052 tail?
c. What do you conclude?
ANS: Answer not provided MSC: New
19. What are the critical values of t for each of the following values of N and alpha using a nondirectional hypothesis?
N
a. 12 0.05
b. 20 0.01
c. 2 0.05
d. 5 0.02
e. 19 0.01
Now using a directional hypothesis?
N
f. 13 0.025
g. 17 0.005
h. 8 0.05
i. 15 0.01
j. 10 0.05
ANS: Answer not provided MSC: New
20. One wishes to investigate the hypothesis that exercise reduces systolic blood pressure. The population mean for the systolic blood pressure of people who do not exercise is 120 mmHg. A sample of 13 members of a local running club has a mean systolic blood pressure of 113 mmHg with a standard deviation of 9.2 mmHg.
a. State H1 (directional)
b. State H0
c. What do you conclude using = .011 tail
d. What is the size of the effect?
ANS: Answer not provided MSC: New
21. Using = 0.052 tail, is it reasonable to assume that the following set of scores could have been randomly drawn from a population with a mean of 74.5?
X: 73.0, 72.1, 72.0, 69.1, 70.8
ANS: Answer not provided MSC: New
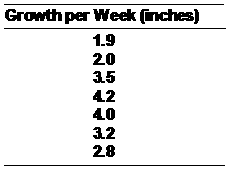
22. The average growth per day of a certain type lawn seed using standard fertilizer is 2.6 inches per week. You wish to test the effects of a fertilizer on growth rate. You add fertilizer to several different patches of grass grown from that seed and observe the following results:
a. What is the value of tobt?
b. What do you conclude using = 0.052 tail?
ANS: Answer not provided MSC: New
23. You believe that sleep affects memory. Having collected data on a large number of subjects who are getting ordinary sleep, you know that the mean digit span of this population is 5.6 digits. To test your hypothesis you measure the digit span of 15 volunteers randomly selected from the population, after depriving them of one night’s sleep. The results show = 4.1 and s = 1.4.
a. What do you conclude, using = 0.052 tail?
b. What is the size of effect?
ANS: Answer not provided MSC: New
24. Consider the following set of scores:
102, 102, 106, 105, 104, 104, 107, 108
a. What is the 95% confidence interval for the population mean?
b. What is the 99% confidence interval for the population mean?
ANS: Answer not provided MSC: New
a. If N = 18, what is the 95% confidence interval for the population mean?
b. If N = 18, what is the 99% confidence interval for the population mean?
c. If N = 10, what is the 95% confidence interval for the population mean?
d. If N = 10, what is the 99% confidence interval for the population mean?
ANS: Answer not provided MSC: New
26. Assume that µ = 500 and = 100. Your study shows a sample of size 22 with a mean of 530 and standard deviation of 113.
a. What is the most powerful test to use to test the hypothesis that the mean of the sample was drawn from the above Null Hypothesis Population?
b. What is the value of the test statistic?
c. What do you conclude using = 0.052 tail?
ANS: Answer not provided MSC: New
27. Using the information in problem 26:
a. What is the value of tobt?
b. Does z or t allow one to reject H0 more easily?
c. What type error might one be making in this problem?
ANS: Answer not provided MSC: New
28. Assume that you have just calculated the correlation coefficient from an experiment with N = 16 pairs of observations. The value of robt is 0.493.
a. What is the value of tobt for testing the hypothesis that r is significantly different from zero?
b. What do you conclude using = 0.052 tail?
c. What is the value of rcrit?
ANS: Answer not provided MSC: New
29. Consider the following set of scores:
| X | 10 | 15 | 20 | 2 | 5 | 30 | 35 |
| Y | 11 | 12 | 16 | 1 | 3 | 19 | 20 |
a. What is the value of the correlation coefficient?
b. What is the value of rcrit using = 0.052 tail?
c. Is robt significantly different from zero using = 0.052 tail?
ANS: Answer not provided MSC: New
30. You conduct a single sample experiment to determine if the cingulate cortex is involved in learning tasks involving choice behavior. Twenty-two rats with lesions of the cingulate cortex are tested in a two choice Y-maze with the correct arm of the maze being randomly determined from trial-to-trial. A signal light illuminates the correct arm on each trial. Assume that cingulate cortex lesions do not interfere with reception of the signal light. Previous research with a large number of rats on this task has shown that the mean number of trials learn the task is 15 trials. The results of the experiment show a mean of 18 trials with a standard deviation of 5.8 for the lesioned rats to learn the task.
a. What is your conclusion, using = 0.052 tail?
b. What is the size of the effect?
ANS: Answer not provided MSC: New
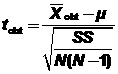
No comments:
Post a Comment